
【题目】工厂接到订单,需要边长为(a+3)和3的两种正方形卡纸.
(1)仓库只有边长为(a+3)的正方形卡纸,现决定将部分边长为(a+3)的正方形纸片,按图甲所示裁剪得边长为3的正方形.
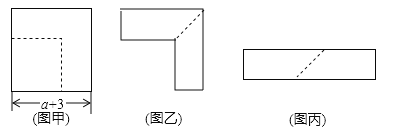
①如图乙,求裁剪正方形后剩余部分的面积(用含a代数式来表示);
②剩余部分沿虚线又剪拼成一个如图丙所示长方形(不重叠无缝隙),则拼成的长方形的边长多少?(用含a代数式来表示);
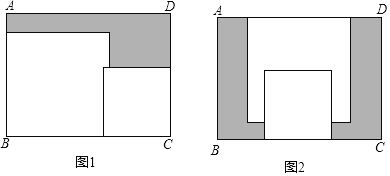
(2)若将裁得正方形与原有正方形卡纸放入长方体盒子底部,按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),盒子底部中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2测得盒子底部长方形长比宽多3,则S2﹣S1的值为 .

【答案】(1)①裁剪正方形后剩余部分的面积=a2+6a;②拼成的长方形的边长分别为a和a+6;(2)9.
【解析】
(1)①根据面积差可得结论;
②根据图形可以直接得结论;
(2)分别计算S2和S1的值,相减可得结论.
(1)①裁剪正方形后剩余部分的面积=(a+3)2﹣32=(a+3﹣3)(a+3+3)=a(a+6)=a2+6a;
②拼成的长方形的宽是:a+3﹣3=a,∴长为a+6,则拼成的长方形的边长分别为a和a+6;
(2)设AB=x,则BC=x+3,∴图1中阴影部分的面积为S1=x(x+3)﹣(a+3)2﹣32+3(a+6﹣x﹣3),图2中阴影部分的面积为S2=x(x+3)﹣(a+3)2﹣32+3(a+6﹣x),∴S2﹣S1的值=3(a+6﹣x)﹣3(a+6﹣x﹣3)=3×3=9.
故答案为:9.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】某商场经销一种商品,已知其每件进价为40元。现在每件售价为70元,每星期可卖出500件。该商场通过市场调查发现:若每件涨价1元,则每星期少卖出10件;若每件降价1元,则每星期多卖出m(m为正整数)件。设调查价格后每星期的销售利润为W元。
(1)设该商品每件涨价x(x为正整数)元,
①若x=5,则每星期可卖出____件,每星期的销售利润为_____元;
②当x为何值时,W最大,W的最大值是多少。
(2)设该商品每件降价y(y为正整数)元,
①写出W与Y的函数关系式,并通过计算判断:当m=10时每星期销售利润能否达到(1)中W的最大值;
②若使y=10时,每星期的销售利润W最大,直接写出W的最大值为_____。
(3)若每件降价5元时的每星期销售利润,不低于每件涨价15元时的每星期销售利润,求m的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民小胡上星期五以每股13.1元的价格买进某种股票1000股,该股票本周的涨跌情况(表格数字表示比前--天涨或跌多少元)如下表(单位:元):
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | -0.3 | 0 | -0.1 | +0.2 | +0.1 |
(1)本周内最高价是每股__________元最低价是每股元_________;
(2)如果小胡在星期五收盘前将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如![]() 就是完全对称式(代数式中
就是完全对称式(代数式中![]() 换成b,b换成
换成b,b换成![]() ,代数式保持不变).下列三个代数式:①
,代数式保持不变).下列三个代数式:①![]() ;②
;②![]() ;③
;③![]() .其中是完全对称式的是( )
.其中是完全对称式的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表(单位:环):

根据表格中的数据,可计算出甲、乙两人的平均成绩都是9(环).
(1)分别计算甲、乙六次测试成绩的方差;
(2)根据数据分析的知识,你认为选 名队员参赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
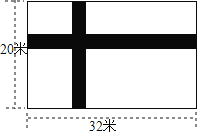
【题目】如图所示,宽为20米,长为32米的长方形地面上,修筑宽度为x米的两条互相垂直的小路,余下的部分作为耕地,如果要在耕地上铺上草皮,选用草皮的价格是每平米a元,
(1)求买草皮至少需要多少元?(用含a,x的式子表示)
(2)计算a=40,x=2时,草皮的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
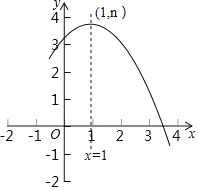
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其顶点坐标为(1,n),且与x轴的一个交点在(3,0)和(4,0)之间,则下列结论:
①ac![]()
②a﹣b+c>0;
③当![]() 时,y随x的增大而增大
时,y随x的增大而增大
若(﹣![]() ,y1),(
,y1),(![]() ,y2)是抛物线上的两点,则y1
,y2)是抛物线上的两点,则y1![]() y2;
y2;
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题9分)据报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.某校学生会想知道学生对这个提议的了解程度,随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
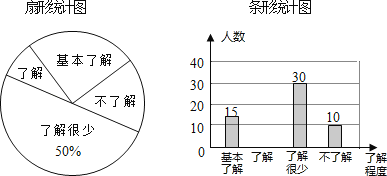
(1)接受问卷调查的学生共有___名,扇形统计图中“基本了解”部分所对应扇形的圆心角为___;请补全条形统计图;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解”和“基本了解”程度的总人数;
(3)“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,请用树状图或列表法求两人打平的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com