
【题目】如图,![]() ,
,![]() ,
,![]() ,
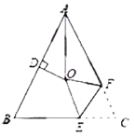
,![]() 的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )
的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
连接OB、OC,根据角平分线的定义求出∠BAO,根据等腰三角形两底角相等求出∠ABC,再根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OB,根据等边对等角可得∠ABO=∠BAO,再求出∠OBC,然后判断出点O是△ABC的外心,根据三角形外心的性质可得OB=OC,再根据等边对等角求出∠OCB=∠OBC,根据翻折的性质可得OE=CE,然后根据等边对等角求出∠COE,再利用三角形内角和定理列式计算即可得出答案.
如图,连接OB、OC,
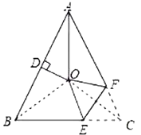
∵![]() ,AO为
,AO为![]() 的平分线
的平分线
∴![]()
又∵![]() ,
,
∴![]()
∵DO是AB的垂直平分线,
∴![]() .
.
∴![]() ,
,
∴![]()
∵DO是AB的垂直平分线,AO为![]() 的平分线
的平分线
∴点О是![]() 的外心,
的外心,
∴![]() ,
,
∴![]() ,
,
∵将![]() 沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合
沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]()


科目:初中数学 来源: 题型:
【题目】宁远县教育局要求各学校加强对学生的安全教育,全县各中小学校引起高度重视,小刚就本班同学对安全知识的了解程度进行了一次调查统计.他将统计结果分为三类,A:熟悉,B:了解较多,C:一般了解.图①和图②是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求小刚所在的班级共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算“了解较多”部分所对应的扇形圆心角的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
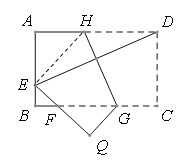
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l:y=(x﹣h)2﹣4(h为常数)
(1)如图1,当抛物线l恰好经过点P(1,﹣4)时,l与x轴从左到右的交点为A、B,与y轴交于点C.
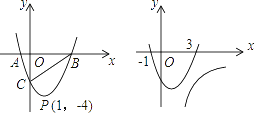
①求l的解析式,并写出l的对称轴及顶点坐标.
②在l上是否存在点D,使S△ABD=S△ABC , 若存在,请求出D点坐标,若不存在,请说明理由.
③点M是l上任意一点,过点M做ME垂直y轴于点E,交直线BC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点M的坐标.
(2)设l与双曲线y=![]() 有个交点横坐标为x0,且满足3≤x0≤5,通过l位置随h变化的过程,直接写出h的取值范围.
有个交点横坐标为x0,且满足3≤x0≤5,通过l位置随h变化的过程,直接写出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明玩抽卡片和旋转盘游戏,有两张正面分别标有数字1,2的不透明卡片,背面完全相同;转盘被平均分成3个相等的扇形,并分别标有数字﹣1,3,4(如图所示),小明把卡片背面朝上洗匀后从中随机抽出一张,记下卡片上的数字;然后转动转盘,转盘停止后,记下指针所在区域内的数字(若指针在分格线上,则重转一次,直到指针指向某一区域内为止).
(1)请用列表法或画树形图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之积为负数的概率.
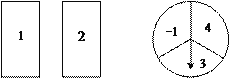
查看答案和解析>>
科目:初中数学 来源: 题型:
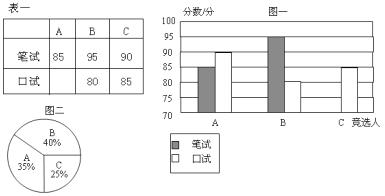
【题目】三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表一和图一:
(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按![]() 的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
查看答案和解析>>
科目:初中数学 来源: 题型:
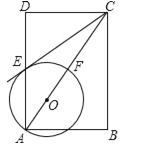
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com