
【题目】已知抛物线l:y=(x﹣h)2﹣4(h为常数)
(1)如图1,当抛物线l恰好经过点P(1,﹣4)时,l与x轴从左到右的交点为A、B,与y轴交于点C.
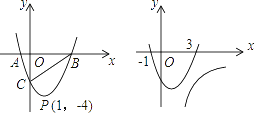
①求l的解析式,并写出l的对称轴及顶点坐标.
②在l上是否存在点D,使S△ABD=S△ABC , 若存在,请求出D点坐标,若不存在,请说明理由.
③点M是l上任意一点,过点M做ME垂直y轴于点E,交直线BC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点M的坐标.
(2)设l与双曲线y=![]() 有个交点横坐标为x0,且满足3≤x0≤5,通过l位置随h变化的过程,直接写出h的取值范围.
有个交点横坐标为x0,且满足3≤x0≤5,通过l位置随h变化的过程,直接写出h的取值范围.
【答案】(1)①抛物线的解析式为y=(x﹣1)2﹣4,抛物线的对称轴为x=1,顶点坐标为(1,﹣4);②(1+![]() ,3)或(1﹣
,3)或(1﹣![]() ,3);③(﹣
,3);③(﹣![]() +1,﹣
+1,﹣![]() )或(
)或(![]() +1,﹣
+1,﹣![]() );(2)当2≤h≤5﹣
);(2)当2≤h≤5﹣![]() 或4≤h≤5+
或4≤h≤5+![]() 时.
时.
【解析】(1)①将P(1,-4)代入得到关于h的方程,从而可求得h的值,可得到抛物线的解析式,然后依据抛物线的解析式可直接得到抛物线的对称轴和顶点坐标;
②先求得OC的长,然后由三角形的面积公式可得到点D的纵坐标为3或-3,最后将y的值代入求得对应的x的值即可;
③先证明四边形OEDF为矩形,则DO=EF,由垂线的性质可知当OD⊥BC时,OD有最小值,即EF有最小值,然后由中点坐标公式可求得点D的坐标,然后可的点M的纵坐标,由函数的关系式可求得点M的横坐标;
(2)抛物线y=(x-h)2-4的顶点在直线y=-4上,然后求得当x=3和x=5时,双曲线对应的函数值,得到点A和点B的坐标,然后分别求得当抛物线经过点A和点B时对应的h的值,然后画出平移后的图象,最后依据图象可得到答案.
(1)①将P(1,﹣4)代入得:(1﹣h)2﹣4=﹣4,解得h=1,
∴抛物线的解析式为y=(x﹣1)2﹣4,
∴抛物线的对称轴为x=1,顶点坐标为(1,﹣4);
②将x=0代入得:y=﹣3,
∴点C的坐标为(0,﹣3),
∴OC=3,
∵S△ABD=S△ABC,
∴点D的纵坐标为3或﹣3,
当y=﹣3时,(x﹣1)2﹣4=﹣3,解得x=2或x=0,
∴点D的坐标为(0,﹣3)或(2,﹣3),
当y=3时,(x﹣1)2﹣4=3,解得:x=1+![]() 或x=1﹣
或x=1﹣![]() ,
,
∴点D的坐标为(1+ ![]() ,3)或(1﹣
,3)或(1﹣ ![]() ,3),
,3),
综上所述,点D的坐标为(0,﹣3)或(2,﹣3)或(1+ ![]() ,3)或(1﹣
,3)或(1﹣ ![]() ,3)时,S△ABD=S△ABC ;
,3)时,S△ABD=S△ABC ;
③如图1所示:
∵∠EOF=∠OED=∠OFD=90°,
∴四边形OEDF为矩形,
∴DO=EF,
依据垂线段的性质可知:当OD⊥BC时,OD有最小值,即EF有最小值,
把y=0代入抛物线的解析式得:(x﹣1)2﹣4=0,解得x=﹣1或x=3,
∴B(3,0),
∴OB=OC,
又∵OD⊥BC,
∴CD=BD,
∴点D的坐标(![]() ,﹣
,﹣![]() ),
),
将y=﹣![]() 代入得:(x﹣1)2﹣4=﹣
代入得:(x﹣1)2﹣4=﹣![]() ,解得x=﹣
,解得x=﹣![]() +1或x=
+1或x= ![]() +1.
+1.
∴点M的坐标为(﹣![]() +1,﹣
+1,﹣![]() )或(
)或( ![]() +1,﹣
+1,﹣![]() )
)
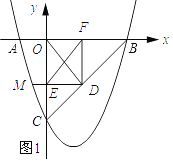
(2)∵y=(x﹣h)2﹣4,
∴抛物线的顶点在直线y=﹣4上,
理由:对双曲线,当3≤x0≤5时,﹣3≤y0≤﹣![]() ,
,
即L与双曲线在A(3,﹣3),B(5,﹣![]() )之间的一段有个交点,
)之间的一段有个交点,
当抛物线经过点A时,(3﹣h)2﹣4=﹣3,解得h=2或h=4,
当抛物线经过点B时,(5﹣h)2﹣4=﹣![]() ,解得:h=5+
,解得:h=5+![]() 或h=5﹣
或h=5﹣ ![]() ,
,
随h的逐渐增加,l的位置随向右平移,如图所示,
由函数图象可知:当2≤h≤5﹣![]() 或4≤h≤5+
或4≤h≤5+![]() 时,抛物线与双曲线在3≤x0≤5段有个交点.
时,抛物线与双曲线在3≤x0≤5段有个交点.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】规定两数a、b之间的一种运算,记作(a,b):如果![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:
(5,125)= ,(-2,4)= ,(-2,-8)= ;
(2)小明在研究这种运算时发现一个现象:![]() ,他给出了如下的证明:
,他给出了如下的证明:
设![]() ,则
,则![]() ,即
,即![]()
∴![]() ,即
,即![]() ,
,
∴![]() .
.
请你尝试运用上述这种方法说明下面这个等式成立的理由.
(4,5)+(4,6)=(4,30)
查看答案和解析>>
科目:初中数学 来源: 题型:
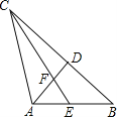
【题目】如图,线段AB,AC是两条绕点A可以自由旋转的线段(但点A,B,C始终不在同一条直线上),已知AB=5,AC=7,点D,E分别是AB,BC的中点,则四边形BEFD面积的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8,AC=6.点D在边AB上,AD=4.5.△ABC的角平分线AE交CD于点F.
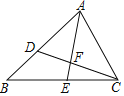
(1)求证:△ACD∽△ABC;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
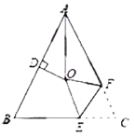
【题目】如图,![]() ,
,![]() ,
,![]() ,
,![]() 的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )
的平分线与AB的垂直平分线交于O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与O点恰好重合,则∠OEC的度数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
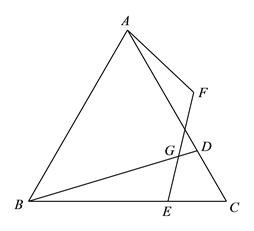
【题目】如图,在等边![]() 中,
中, ![]() 分别是边
分别是边![]() 上的点,且
上的点,且![]() ,
,![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,
,![]() 交
交![]() 于
于![]() .
.
(1)连接![]() ,则
,则![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)若![]() ,求
,求![]() 的大小(用
的大小(用![]() 的式子表示)
的式子表示)
(2)用等式表示线段![]() 和
和![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F,若小敏行走的路程为3100m,则小聪行走的路程为( )m.
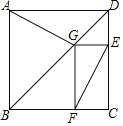
A.3100B.4600C.3000D.3600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 ![]() =n.
=n.
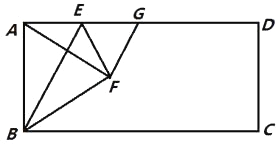
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式:①a0=1;②a2a3=a5;③2﹣2=﹣![]() ;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2,其中正确的是( )
;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2,其中正确的是( )
A、①②③B、①③⑤
C、②③④D、②④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com