
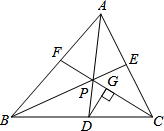
 如图,已知点P为△ABC三条内角平分线AD、BE、CF的交点,作DG⊥PC于G,则∠PDG等于
如图,已知点P为△ABC三条内角平分线AD、BE、CF的交点,作DG⊥PC于G,则∠PDG等于 ∠BAC+∠ABC,由DG⊥PC,得出∠GDC=90°-
∠BAC+∠ABC,由DG⊥PC,得出∠GDC=90°- ∠ACB,而∠PDC=∠PDG+∠GDC,把∠PDG再进一步用∠BAC+∠ABC表示,整理得出结论即可.
∠ACB,而∠PDC=∠PDG+∠GDC,把∠PDG再进一步用∠BAC+∠ABC表示,整理得出结论即可. ∠ABC,∠BAD=
∠ABC,∠BAD= ∠BAC,∠GCD=
∠BAC,∠GCD= ∠ACB,
∠ACB, ∠BAC+∠ABC,∠PDC=∠PDG+90°-∠BCF=∠PDG+90°-
∠BAC+∠ABC,∠PDC=∠PDG+90°-∠BCF=∠PDG+90°- ∠ACB=∠PDG+90°-
∠ACB=∠PDG+90°- (180°-∠BAC-∠ABC),
(180°-∠BAC-∠ABC), ∠BAC+∠ABC=∠PDG+90°-
∠BAC+∠ABC=∠PDG+90°- (180°-∠BAC-∠ABC),
(180°-∠BAC-∠ABC), ∠ABC=∠ABE.
∠ABC=∠ABE.

科目:初中数学 来源: 题型:
 如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.
如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.查看答案和解析>>
科目:初中数学 来源: 题型:
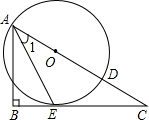 (2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设| BA |
| a |
| BC |
| b |
| BD |
| a |
| b |
| a |
| b |
| BD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=
如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com