
【题目】如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1 , S2 , 则S2﹣S1= . 
【答案】2 ![]() ﹣π
﹣π
【解析】解:连接BE, ∵以点B为圆心的扇形与边CD相切于点E,
∵在菱形ABCD中,∠A=60°,AB=4,
∴BE⊥CD,
∵点E是CD的中点,
∴CE= ![]() CD=2,BE=2
CD=2,BE=2 ![]() ,∠EBC=30°,
,∠EBC=30°,
∵扇形的圆心角为60°,
∴S2﹣S1= ![]() ×CEBE﹣
×CEBE﹣ ![]() =
= ![]() 2×2
2×2 ![]() ﹣π=2
﹣π=2 ![]() ﹣π.
﹣π.
所以答案是:2 ![]() ﹣π.
﹣π.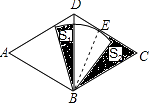
【考点精析】本题主要考查了菱形的性质和切线的性质定理的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=1,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度![]() 与所挂物体的质量
与所挂物体的质量![]() 之间有如下表关系:
之间有如下表关系:
|
|
|
|
|
| … |
|
|
|
|
|
| … |
下列说法不正确的是( )
A. ![]() 随
随![]() 的增大而增大 B. 所挂物体质量每增加
的增大而增大 B. 所挂物体质量每增加![]() 弹簧长度增加
弹簧长度增加![]()
C. 所挂物体为![]() 时,弹簧长度为
时,弹簧长度为![]() D. 不挂重物时弹簧的长度为
D. 不挂重物时弹簧的长度为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )

A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知小华家、小夏家、小红家及学校在同一条大路旁,一天,他们放学后从学校出发,先向南行1000m到达小华家A处,继续向北行3000m到达小红B家处,然后向南行6000m到小夏家C处.
(1)以学校以原点,以向南方向为正方向,用1个单位长度表示1000m,请你在数轴上表示出小华家、小夏家、小红家的位置;
(2)小红家在学校什么位置?离学校有多远?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com