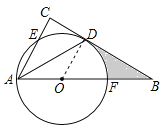
【题目】如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．

（1）试判断直线BC与⊙O的位置关系，并说明理由；

（2）若BD=，BF=2，求阴影部分的面积（结果保留π）．

参考答案：

【答案】（1）BC与⊙O相切；（2）．

【解析】

试题分析：（1）连接OD，证明OD∥AC，即可证得∠ODB=90°，从而证得BC是圆的切线；

（2）在直角三角形OBD中，设OF=OD=x，利用勾股定理列出关于x的方程，求出方程的解得到x的值，即为圆的半径，求出圆心角的度数，直角三角形ODB的面积减去扇形DOF面积即可确定出阴影部分面积．

试题解析：（1）BC与⊙O相切．

证明：连接OD．∵AD是∠BAC的平分线，∴∠BAD=∠CAD．又∵OD=OA，∴∠OAD=∠ODA，∴∠CAD=∠ODA，∴OD∥AC，∴∠ODB=∠C=90°，即OD⊥BC．又∵BC过半径OD的外端点D，∴BC与⊙O相切；

（2）设OF=OD=x，则OB=OF+BF=x+2，根据勾股定理得：，即，解得：x=2，即OD=OF=2，∴OB=2+2=4，∵Rt△ODB中，OD=OB，∴∠B=30°，∴∠DOB=60°，∴S扇形AOB==，则阴影部分的面积为S△ODB﹣S扇形DOF==．

故阴影部分的面积为．

关闭