Question

【题目】如图，抛物线y=x2+bx﹣2与x轴交于A、B两点，与y轴交于C点，且A（﹣1，0）．

（1）求抛物线的解析式及顶点D的坐标；

（2）判断△ABC的形状，证明你的结论；

（3）点M是x轴上的一个动点，当△DCM的周长最小时，求点M的坐标．

Answer 1

【答案】（1）, D (,);（2）△ABC是直角三角形,证明见解析;

（3）M（ ，0）.

【解析】（1）∵点A（-1，0）在抛物线y=x2 + bx-2上，

∴× (-1 )2 + b× (-1)–2 = 0，

解得b =，

∴ 抛物线的解析式为y=x2-x-2.

y= ( x2 -3x- 4 ) =(x-)2-,

∴顶点D的坐标为 (, -).

（2）当x = 0时y = -2,

∴C（0，-2），OC = 2。

当y = 0时， x2-x-2 = 0，

∴x1 =-1， x2 = 4,

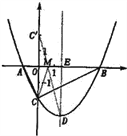
∴B (4,0)

∴OA = 1, OB = 4, AB = 5.

∵AB2 = 25, AC2 = OA2 + OC2 = 5, BC2 = OC2 + OB2 = 20,

∴AC2 +BC2 = AB2.

∴△ABC是直角三角形.

（3）作出点C关于x轴的对称点C′，则C′（0，2），OC′=2，连接C′D交x轴于点M，根据轴对称性及两点之间线段最短可知，MC + MD的值最小及△DCM的周长最小

设抛物线的对称轴交x轴于点E.

∵ED∥y轴, ∴∠OC′M=∠EDM,∠C′OM=∠DEM

∴△C′OM∽△DEM.

∴

∴， ∴m =．

所以M的坐标为（，0）