
【题目】某商店需要购进甲、乙两种商品共130件,其进价和获利情况如下表:

(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于3000元,且销售完这批商品后总获利多于1048元,请问有哪些购货方案?
【答案】(1)甲种商品购进50件,乙种商品购进80件;(2)有两种购货方案:方案一:甲种商品购进61件,乙种商品购进69件;方案二:甲种商品购进62件,乙种商品购进68件.
【解析】
(1)设甲种商品应购进x件,乙种商品应购进y件,根据购进甲、乙两种商品共130件且销售完这批商品后能获利1100元,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设甲种商品购进a件,则乙种商品购进(130-a)件,根据购货资金少于3000元且销售完这批商品后获利多于1048元,即可得出关于a的一元一次不等式组,解之即可得出a的取值范围,取其内的整数即可得出各购货方案.
(1)设甲种商品应购进x件,乙种商品应购进y件.
根据题意得:![]() ,
,
解得:![]() .
.
答:甲种商品购进50件,乙种商品购进80件.
(2)设甲种商品购进a件,则乙种商品购进(130-a)件.
根据题意得: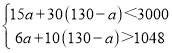 ,
,
解得:60<a<63.
∵a为非负整数,
∴a取61,62,
∴130-a相应取69,68.
答:有两种购货方案:方案一:甲种商品购进61件,乙种商品购进69件;方案二:甲种商品购进62件,乙种商品购进68件.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点.

(1)求证:四边形EGFH是菱形;
(2)若AB=1,则当∠ABC+∠DCB=90°时,求四边形EGFH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在8×8的网格中的每个小正方形边长都是1,线段交点称作格点.任意连接这些格点,可得到一些线段.按要求作图:
(1)请画出△ABC的高AD;
(2)请连接格点,用一条线段将图中△ABC分成面积相等的两部分;
(3)直接写出△ABC的面积是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
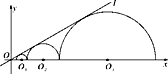
【题目】如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线l相切.设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当直线l与x轴所成锐角为30°,且r1=1时,r2018=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解不等式![]() 的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
的过程如图,请指出他解答过程中错误步骤的序号,并写出正确的解答过程.
解:去分母,得3(1+x)-2(2x+1)≤1.①
去括号,得3+3x-4x+1≤1.②
移项,得3x-4x≤1-3-1.③
合并同类项,得-x≤-3.④
两边都除以-1,得x≤3.⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探究函数y=x+![]() 的图象与性质】
的图象与性质】
(1)函数y=x+![]() 的自变量x的取值范围是________;
的自变量x的取值范围是________;
(2)下列四个函数图象中,函数y=x+![]() 的图象大致是________;
的图象大致是________;

(3)对于函数y=x+![]() ,求当x>0时,y的取值范围.请将下列的求解过程补充完整.
,求当x>0时,y的取值范围.请将下列的求解过程补充完整.
解:∵x>0,∴y=x+![]() =(
=(![]() )2+
)2+![]() =
=![]() +________.
+________.
∵![]() ≥0,∴y≥________.
≥0,∴y≥________.
【拓展运用】
(4)若函数y=![]() ,求y的取值范围.
,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N.连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com