
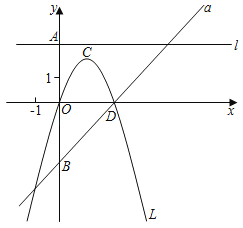
【题目】如图,若b是正数.直线l:y=b与y轴交于点A,直线a:y=x﹣b与y轴交于点B;抛物线L:y=﹣x2+bx的顶点为C,且L与x轴右交点为D.
(1)若AB=6,求b的值,并求此时L的对称轴与a的交点坐标;
(2)当点C在l下方时,求点C与l距离的最大值;
(3)设x0≠0,点(x0,y1),(x0,y2),(x0,y3)分别在l,a和L上,且y3是y1,y2的平均数,求点(x0,0)与点D间的距离;
(4)在L和a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出b=2019和b=2019.5时“美点”的个数.
【答案】(1)L的对称轴x=1.5,L的对称轴与a的交点为(1.5,﹣1.5 );(2)1;(3)![]() ;(4)b=2019时“美点”的个数为4040个,b=2019.5时“美点”的个数为1010个.
;(4)b=2019时“美点”的个数为4040个,b=2019.5时“美点”的个数为1010个.
【解析】
(1)当x=0时,y=x﹣b=﹣b,所以B (0,﹣b),而AB=6,而A(0,b),则b﹣(﹣b)=6,b=3.所以L:y=﹣x2+3x,对称轴x=1.5,当x=1.5吋,y=x﹣3=﹣1.5,于是得到结论.
(2)由y=﹣(x﹣![]() )2+
)2+![]() ,得到L的顶点C(
,得到L的顶点C(![]() ,
,![]() ),由于点C在l下方,于是得到结论;
),由于点C在l下方,于是得到结论;
(3)由題意得到y3=![]() ,即y1+y2=2y3,得b+x0﹣b=2(﹣x02+bx0)解得x0=0或x0=b﹣
,即y1+y2=2y3,得b+x0﹣b=2(﹣x02+bx0)解得x0=0或x0=b﹣![]() .但x0≠0,取x0=b﹣
.但x0≠0,取x0=b﹣![]() ,得到右交点D(b,0).于是得到结论;
,得到右交点D(b,0).于是得到结论;
(4)①当b=2019时,抛物线解析式L:y=﹣x2+2019x直线解析式a:y=x﹣2019,美点”总计4040个点,②当b=2019.5时,抛物线解析式L:y=﹣x2+2019.5x,直线解析式a:y=x﹣2019.5,“美点”共有1010个.
解:(1)当x=0时,y=x﹣b=﹣b,
∴B (0,﹣b),
∵AB=6,而A(0,b),
∴b﹣(﹣b)=6,
∴b=3.
∴L:y=﹣x2+3x,
∴L的对称轴x=1.5,
当x=1.5吋,y=x﹣3=﹣1.5,
∴L的对称轴与a的交点为(1.5,﹣1.5 );
(2)y=﹣(x﹣![]() )2+
)2+![]()
∴L的顶点C(img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/27/16/06e66ec6/SYS202011271613427160598622_DA/SYS202011271613427160598622_DA.002.png" width="16" height="41" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,![]() ),
),
∵点C在l下方,
∴C与l的距离b﹣![]() =﹣
=﹣![]() (b﹣2)2+1≤1,
(b﹣2)2+1≤1,
∴点C与1距离的最大值为1;
(3)由题意得y3=![]() ,即y1+y2=2y3,
,即y1+y2=2y3,
得b+x0﹣b=2(﹣x02+bx0)
解得x0=0或x0=b﹣![]() .但x0≠0,取x0=b﹣
.但x0≠0,取x0=b﹣![]() ,
,
对于L,当y=0吋,0=﹣x2+bx,即0=﹣x(x﹣b),
解得x1=0,x2=b,
∵b>0,
∴右交点D(b,0).
∴点(x0,0)与点D间的距离b﹣(b﹣![]() )=
)=![]() ;
;
(4)①当b=2019时,抛物线解析式L:y=﹣x2+2019x,
直线解析式a:y=x﹣2019
联立上述两个解析式可得:x1=﹣1,x2=2019,
∴可知每一个整数x的值都对应的一个整数y值,且﹣1和2019之间(包括﹣1和﹣2019)共有2021个整数;
∵另外要知道所围成的封闭图形边界分两部分:线段和抛物线,
∴线段和抛物线上各有2021个整数点,
∴总计4042个点,
∵这两段图象交点有2个点重复,
∴美点”的个数:4042﹣2=4040(个);
②当b=2019.5时,
抛物线解析式L:y=﹣x2+2019.5x,
直线解析式a:y=x﹣2019.5,
联立上述两个解析式可得:x1=﹣1,x2=2019.5,
∴当x取整数时,在一次函数y=x﹣2019.5上,y取不到整数值,因此在该图象上“美点”为0,
在二次函数y=x2+2019.5x图象上,当x为偶数时,函数值y可取整数,
可知﹣1到2019.5之 间有1010个偶数,因此“美点”共有1010个.
故b=2019时“美点”的个数为4040个,b=2019.5时“美点”的个数为1010个.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为 60°,然后在坡顶D测得树顶B的仰角为300,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( ) m

A. ![]() B. 30 C.
B. 30 C. ![]() D. 40
D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
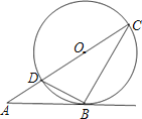
【题目】如图,DC是⊙O的直径,点B在圆上,直线AB交CD延长线于点A,且∠ABD=∠C.
(1)求证:AB是⊙O的切线;
(2)若AB=4cm,AD=2cm,求tanA的值和DB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别是A(﹣4,1),B(﹣1,2),C(﹣2,4).
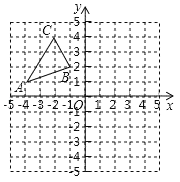
(1)将△ABC向右平移4个单位后得到△A1B1C1,请画出△A1B1C1,并写出点B1的坐标;
(2)△A2B2C2和△A1B1C1关于原点O中心对称,请画出△A2B2C2,并写出点C2的坐标;
(3)连接点A和点B2,点B和点A2,得到四边形AB2A2B,试判断四边形AB2A2B的形状(无须说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
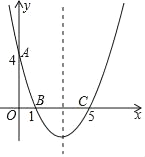
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0)
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)该抛物线有一点D(x,y),使得S△ABC=S△DBC,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC, ∠BAC <60°,将线段 AB 绕点 A逆时针旋转 60°得到点 D, 点 E 与点 D 关于直线 BC 对称,连接 CD,CE,DE.
(1)依题意补全图形;
(2)判断△CDE 的形状,并证明;
(3)请问在直线CE上是否存在点 P,使得 PA - PB =CD 成立?若存在,请用文字描述出点 P 的准确位置,并画图证明;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在 点
在 点![]() 左侧),对称轴为直线
左侧),对称轴为直线![]() .
.
(1)![]() 的值为 ,在坐标系中利用描点法画出此抛物线;
的值为 ,在坐标系中利用描点法画出此抛物线;
| ··· | ··· | |||||
| ··· | ··· |
(2)若直线![]() 过点
过点![]() 且与抛物线交于点
且与抛物线交于点![]() ,请根据图象写出:当
,请根据图象写出:当![]() 时,
时,![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,D是线段AC上一点(不与A,C重合),连接BD,将
,D是线段AC上一点(不与A,C重合),连接BD,将![]() 沿AB翻折,使点D落在点E处,延长BD与EA的延长线交于点F,若
沿AB翻折,使点D落在点E处,延长BD与EA的延长线交于点F,若![]() 是直角三角形,则AF的长为_________.
是直角三角形,则AF的长为_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com