
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在 点
在 点![]() 左侧),对称轴为直线
左侧),对称轴为直线![]() .
.
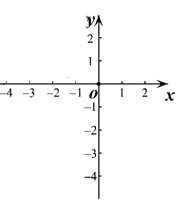
(1)![]() 的值为 ,在坐标系中利用描点法画出此抛物线;
的值为 ,在坐标系中利用描点法画出此抛物线;
| ··· | ··· | |||||
| ··· | ··· |
(2)若直线![]() 过点
过点![]() 且与抛物线交于点
且与抛物线交于点![]() ,请根据图象写出:当
,请根据图象写出:当![]() 时,
时,![]() 的取值范围是 .
的取值范围是 .
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
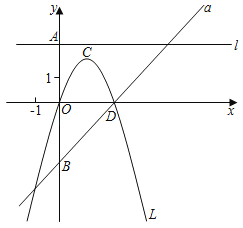
【题目】如图,若b是正数.直线l:y=b与y轴交于点A,直线a:y=x﹣b与y轴交于点B;抛物线L:y=﹣x2+bx的顶点为C,且L与x轴右交点为D.
(1)若AB=6,求b的值,并求此时L的对称轴与a的交点坐标;
(2)当点C在l下方时,求点C与l距离的最大值;
(3)设x0≠0,点(x0,y1),(x0,y2),(x0,y3)分别在l,a和L上,且y3是y1,y2的平均数,求点(x0,0)与点D间的距离;
(4)在L和a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出b=2019和b=2019.5时“美点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形 ABCD 中,过点 A 作 AE⊥DC 交 DC 的延长线于点 E,过点 D 作DF // EA 交 BA 的延长线于点 F.
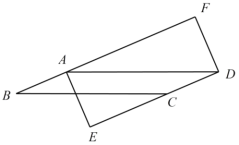
(1)求证:四边形 AEDF 是矩形;
(2)连接BD,若 AB=AE=2,tan FAD ![]() ,求 BD 的长.
,求 BD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+4x+c(a≠0)经过点A(3,﹣4)和B(0,2).
(1)求抛物线的表达式和顶点坐标;
(2)将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线x=3翻折,得到图象N.若过点C(9,4)的直线y=kx+b与图象M、图象N都相交,且只有两个交点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=![]() ,则△EFC的周长为_____________.
,则△EFC的周长为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
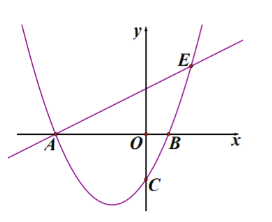
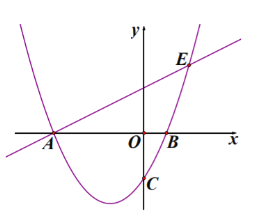
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线的另一个点为点
交抛物线的另一个点为点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
![]() 求
求![]() 和
和![]() 的值.
的值.
![]() 点
点![]() 在直线
在直线![]() 下方的抛物线上任一点,点
下方的抛物线上任一点,点![]() 的横坐标为
的横坐标为![]() 过点
过点![]() 作
作![]() 轴,交
轴,交![]() 于点
于点![]() 设
设![]() 求出
求出![]() 与
与![]() 的函数关系式,并直接写出
的函数关系式,并直接写出![]() 的取值范围.
的取值范围.
![]() 在
在![]() 问的条件下,过点
问的条件下,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,若
,若![]() 把
把![]() 分 成面积比为
分 成面积比为![]() 的两个三角形,求出此时
的两个三角形,求出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )

A.30°B.35°C.40°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
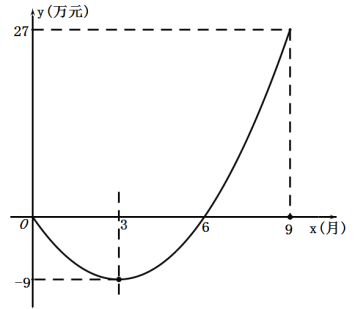
【题目】大学生小李和同学一起自主创业开办了一家公司,公司对经营的盈亏情况在每月的最后一天结算一次.在1-12月份中,该公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数关系.
(1)求y与x函数关系式.
(2)该公司从哪个月开始“扭亏为盈”(当月盈利)? 直接写出9月份一个月内所获得的利润.
(3)在前12 个月中,哪个月该公司所获得利润最大?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com