
【题目】如图1,将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起.
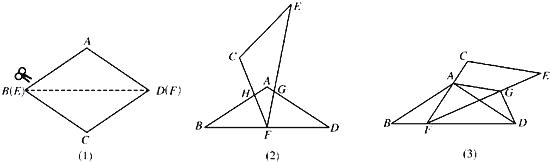
(1)操作:如图2,将△ECF的顶点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,设旋转时FC交BA于点H(H点不与B点重合),FE交DA于点G(G点不与D点重合).
求证:BHGD=BF2
(2)操作:如图3,△ECF的顶点F在△ABD的BD边上滑动(F点不与B、D点重合),且CF始终经过点A,过点A作AG∥CE,交FE于点G,连接DG.
探究:FD+DG= .请予证明.
【答案】(1)证明见解析(2)BD
【解析】
试题分析:(1)根据菱形的性质以及相似三角形的判定得出△BFH∽△DGF,即可得出答案;
(2)利用已知以及平行线的性质证明△ABF≌△ADG,即可得出FD+DG的关系.
试题解析:(1)∵将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,
∴∠B=∠D,
∵将△ECF的顶点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,
∴BF=DF,
∵∠HFG=∠B,
又∵∠HFD=∠HFG+∠GFD=∠B+∠BHF
∴∠GFD=∠BHF,
∴△BFH∽△DGF,
∴![]() ,
,
∴BHGD=BF2;
(2)∵AG∥CE,
∴∠FAG=∠C,
∵∠CFE=∠CEF,
∴∠AGF=∠CFE,
∴AF=AG,
∵∠BAD=∠C,
∴∠BAF=∠DAG,
又∵AB=AD,
∴△ABF≌△ADG,
∴FB=DG,
∴FD+DG=BD,
故答案为:BD.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=ax+b(a<0)的图象与x的交点坐标是(3,0),那么关于x的方程ax+b=0的解是 ______,关于x的不等式ax+b>0的解集是_______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
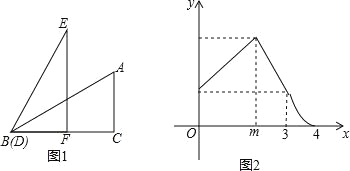
【题目】如图1,两个全等的△ABC和△DEF中,∠ACB=∠DFE=90°,AB=DE,其中点B和点D重合,点F在BC上,将△DEF沿射线BC平移,设平移的距离为x,平移后的图形与△ABC重合部分的面积为y,y关于x的函数图象如图2所示(其中0≤x≤m,m<x≤3,3<x≤4时,函数的解析式不同)
(1)填空:BC的长为 ;
(2)求y关于x的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列关于x的单项式,探究其规律:
x,3x2 , 5x3 , 7x4 , 9x5 , 11x6 , …
按照上述规律,第2015个单项式是( )
A.2015x2015
B.4029x2014
C.4029x2015
D.4031x2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,某地向武汉捐赠口罩1200000只,其中数1200000用科学记数法表示是( )
A.12×105B.12×106C.1.2×105D.1.2×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B的度数相比( )
A.增加了10%
B.减少了10%
C.增加了(1+10%)
D.没有改变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com