
如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足 =
= ,
,
过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点.
(1)求证:AE⊥DE;
(2)若tan∠CBA=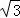 ,AE=3,求AF的长.
,AE=3,求AF的长.
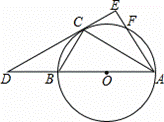
(1)证明:连接OC,
∵OC=OA,
∴∠BAC=∠OCA,
 ∵
∵ =
= ,
,
∴∠BAC=∠EAC,
∴∠EAC=∠OCA,
∴OC∥AE, 3分
∵DE切⊙O于点C,
∴OC⊥DE,
∴AE⊥DE; 6分
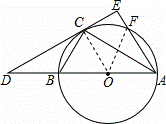
(2)解:∵AB是⊙O的直径,
∴△ABC是直角三角形,
∵tan∠CBA= ,
,
∴∠CBA=60°,
∴∠BAC=∠EAC=30°,
∵△AEC为直角三角形,AE=3,
∴AC=2 ,
,  9分
9分
连接OF,
∵OF=OA,∠OAF=∠BAC+∠EAC=60°,
∴△OAF为等边三角形,
∴AF=OA=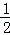 AB,
AB,
 在Rt△ACB中,AC=2
在Rt△ACB中,AC=2 ,tan∠CBA=
,tan∠CBA= ,
,
∴BC=2,(直接给出AF=2不扣分)
∴AB=4,
∴AF=2. 12分


科目:初中数学 来源: 题型:
小明和小丽用形状大小相同、面值不同的5张邮票设计了一个游戏,将面值1元、2元、3元的邮票各一张装入一个信封,面值4元、5元的邮票各一张装入另一个信封.游戏规定:分别从两个信封中各抽取1张邮票,若它们的面值和是偶数,则小明赢;若它们的面值和是奇数,则小丽赢. 请你判断这个游戏是否公平,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
从下列4个命题中任取一个 ①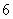 的平方根是
的平方根是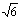
 ; ②
; ②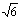 是方程x2﹣6=0的
是方程x2﹣6=0的
解; ③如果两个图形是位似图形,则这两个图形一定相似;④在半径为4的
圆中,15°的圆周角所对的弧长为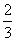 π;是真命题的概率是 .
π;是真命题的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在 平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函
平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函
数y= 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.
(1)求k和b的值;
(2)求△OAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
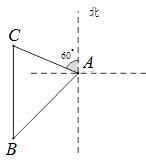
如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行. 当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处. 若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com