
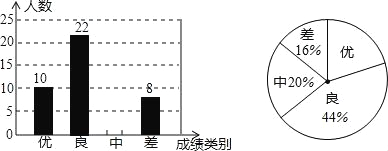
【题目】为迎接2019年中考,对道里区西部优质教育联盟九年级学生进行了一次数学期中模拟考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请你根据统计图中提供的信息解答下列问题:
(1)这次被调查的学生共有多少人,并将条形统计图补充完整:
(2)在扇形统计图中,求出“优”所对应的圆心角度数;
(3)若该联盟九年级共有1050人参加了这次数学考试,估计九年级这次考试共有多少名学生的数学成绩可以达到优秀?
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面内,直线y=-x+5与![]() 轴和
轴和![]() 轴分别交于A、B两点,二次函数y=
轴分别交于A、B两点,二次函数y=![]() +bx+c的图象经过点A、B,且顶点为C.
+bx+c的图象经过点A、B,且顶点为C.
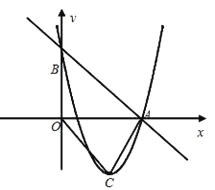
(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且![]() ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有编号分别为1、2、3的球(除编号以为,其余都相同),其中1号球1个,3号球3个,从中随机摸出一个球是2号球的概率为![]() .
.
(1)求袋子里2号球的个数.
(2)甲、乙两人分别从袋中摸出一个球(不放回),甲摸出球的编号记为x,乙摸出球的编号记为y,用列表法求点A(x,y)在直线y=x下方的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
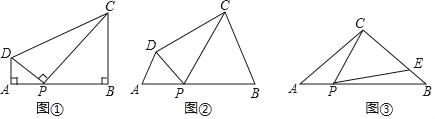
【题目】(感知)如图①,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC=90°.易证:△DAP∽△PBC(不要求证明).
(探究)如图②,在四边形ABCD中,点P在边AB上(点P不与点A、B重合),∠A=∠B=∠DPC.
(1)求证:△DAP~△PBC.
(2)若PD=5,PC=10,BC=9,求AP的长.
(应用)如图③,在△ABC中,AC=BC=4,AB=6,点P在边AB上(点P不与点A、B重合),连结CP,作∠CPE=∠A,PE与边BC交于点E.当CE=3EB时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总数排列名次,在规定时间内每人踢100个以上(含100个)为优秀,下表是成绩最好的甲、乙两班各5名学生的比赛数据.(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
乙班 | 100 | 96 | 110 | 90 | 104 | 500 |
统计发现两班总数相等,此时有人建议,可以通过考查数据中的其他信息来评判.试从两班比赛数据的中位数、方差、优秀率三个方面考虑,你认为应该选定哪一个班为冠军?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )
A. ![]() B. 5 C. 4 D.
B. 5 C. 4 D. ![]()
【答案】B
【解析】由旋转的性质可知,在图乙中,∠BCE1=15°,∠D1CE1=60°,AB=6,CD1=CD=7,
∴∠D1CB=60°-15°=45°,
又∵∠ACB=90°,
∴CO平分∠ACB,
又∵AC=BC,
∴CO⊥AB,且CO=AO=BO=![]() AB=3,
AB=3,
∴D1O=CD1-CO=7-3=4,∠AOD1=90°,
∴在Rt△AOD1中,AD1=![]() .
.
故选B.
点睛:本题解题的关键是由旋转的性质证明:∠D1CB=45°,从而得到CD1平分∠ACB,结合等腰三角形的“三线合一”证得∠AOD1=90°,并求得AO=3,OD1=4;这样问题就变得很简单了.
【题型】单选题
【结束】
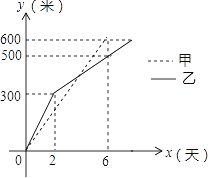
10
【题目】我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同;
④甲队比乙队提前2天完成任务.
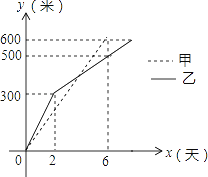
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
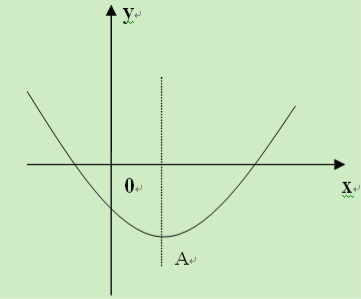
【题目】(本小题满分10分)已知二次函数![]()
(1)当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围。
的取值范围。
(2)以抛物线![]() 的顶点
的顶点![]() 为一个顶点作该抛物线的内接正三角形
为一个顶点作该抛物线的内接正三角形![]() (
(![]() ,
,![]() 两点在抛物线上),请问:△
两点在抛物线上),请问:△![]() 的面积是与
的面积是与![]() 无关的定值吗?若是,请求出这个定值;若不是,请说明理由。
无关的定值吗?若是,请求出这个定值;若不是,请说明理由。
(3)若抛物线![]() 与
与![]() 轴交点的横坐标均为整数,求整数
轴交点的横坐标均为整数,求整数![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
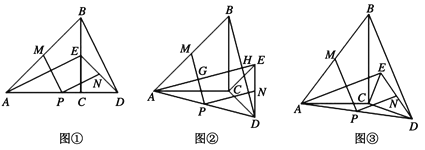
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)请直接写出PM与PN的数量关系及位置关系 ;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请直接写出PM与PN的数量关系及位置关系 ;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com