
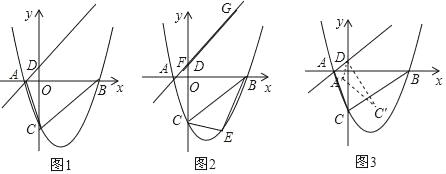
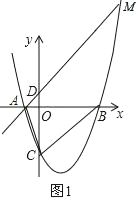
【题目】如图1,抛物线y=![]() x2﹣
x2﹣![]() x﹣3,与x轴交于A和B两点(点A在点B的左侧),与y轴交于点C,过点A的直线与抛物线在第一象限的交点M的横坐标为
x﹣3,与x轴交于A和B两点(点A在点B的左侧),与y轴交于点C,过点A的直线与抛物线在第一象限的交点M的横坐标为![]() ,直线AM与y轴交于点D,连接BC、AC.
,直线AM与y轴交于点D,连接BC、AC.
(1)求直线AD和BC的解折式;
(2)如图2,E为直线BC下方的抛物线上一点,当△BCE的面积最大时,一线段FG=4![]() (点F在G的左侧)在直线AM上移动,顺次连接B、E、F、G四点构成四边形BEFG,请求出当四边形BEFG的周长最小时点F的坐标;
(点F在G的左侧)在直线AM上移动,顺次连接B、E、F、G四点构成四边形BEFG,请求出当四边形BEFG的周长最小时点F的坐标;
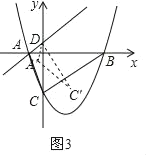
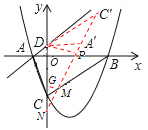
(3)如图3,将△DAC绕点D逆时针旋转角度α(0°<α<180°),记旋转中的三角形为△DA′C′,若直线A′C′分别与直线BC、y轴交于M、N,当△CMN是等腰三角形时,请直接写出CM的长度.
【答案】(1)y=x+1,y=![]() x﹣3;(2)F(
x﹣3;(2)F(![]() ,
,![]() );(3)
);(3)![]() ,
,![]() ,
,![]() 或
或![]() .
.
【解析】
(1)令y=0,得x1=-1,x2=4,A(-1,0),B(4,0),令x=0,得C(0,-3),令x=![]() ,得y=
,得y=![]() ,M(
,M(![]() ,
,![]() ),待定系数法可求直线AD、BC的解析式;
),待定系数法可求直线AD、BC的解析式;
(2)点F是直线BC下方抛物线上的动点,△FBC面积最大值可以转化为求二次函数最大值问题,设点F横坐标为t,则可以将△FBC面积表示成t的二次函数,再应用配方法将二次函数化成顶点式,就可以求出△FBC面积最大时,F的坐标;四边形BEFG周长的最大值实际上就是求EF+BG的最大值,通过轴对称求线段和的最小值方法求解;
(3)△CMN是等腰三角形,必须分三种不同情况讨论:①CM=CN,②CM=MN,③CN=MN.
解:(1)在抛物线y=![]() 中,令x=0,得y=﹣3,
中,令x=0,得y=﹣3,
∴C(0,﹣3),
令y=0,得![]() ,解得x1=﹣1,x2=4,
,解得x1=﹣1,x2=4,
∴A(﹣1,0),B(4,0),
令x=![]() ,得y=
,得y=![]() =
=![]() ,
,
∴M(![]() ,
,![]() ),
),
设直线AD的解析式为y=k1x+b1,将A(﹣1,0),M(![]() ,
,![]() )代入得
)代入得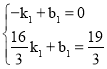 ,
,
解得![]() ,
,
∴直线AD的解析式为y=x+1.
设直线BC的解析式为y=k2x+b2,将B(4,0),C(0,﹣3)代入,得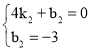 ,
,
解得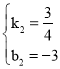 ,
,
∴直线BC的解析式为y=![]() x﹣3;
x﹣3;
(2)如图2,过点E作EH∥y轴交BC于H,

设E(t,![]() ),H(t,
),H(t,![]() ),
),
∴HE=![]() =
=![]()
∴![]() =
=![]() =
=![]() =
=![]()
∵![]() <0,
<0,
∴当t=2时,S△BCE的最大值=6,此时E(2,![]() ),
),
作点B关于直线y=x+1的对称点B1,连接B1G,过点F作B2F∥B1G,且B2F=B1G,
∴B1(﹣1,5),
∵FG=4![]() ,且FG在直线y=x+1上,
,且FG在直线y=x+1上,
∴F可以看作是G向左平移4个单位,向下平移4个单位后的对应点,
∴B2(﹣5,1),
当B2、F、E三点在同一直线上时,BEFG周长最小,设直线B2E解析式为y=mx+n,将B2(﹣5,1),E(2,![]() )分别代入,得
)分别代入,得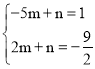 ,
,
解得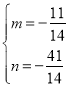 ,
,
∴直线B2E解析式为y=![]() ,
,
联立方程组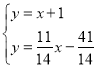 ,
,
解得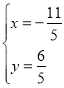 .
.
∴F(![]() ,
,![]() ).
).
(3)如图,分三种情况:
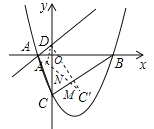
在![]() 中,令
中,令![]() ,则
,则![]()
![]()
![]()
![]()
![]() ,
,
设AC边上的高为h,根据等面积法得,![]()
![]()
![]() 且OB⊥OC,
且OB⊥OC,
![]()
①CM=MN时,如图,过点M作MG⊥OC,过点D作DP⊥MN于点P
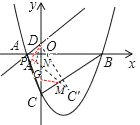
![]()
∴设![]() ,则
,则![]() ,
,
由勾股定理得,![]() ,
,
![]()
![]()
![]() ,即
,即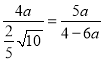
解得,![]() ,
,![]() (舍去)
(舍去)
![]()
②当![]() 时,如图,过点M作MG⊥OC,过点D作DP⊥MN于点P
时,如图,过点M作MG⊥OC,过点D作DP⊥MN于点P

![]()
设![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
![]()
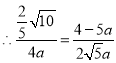 ,解得:
,解得:![]() (舍去),
(舍去),![]() ,
,
![]() ;
;
③当![]() 时,如图,作
时,如图,作![]() ,
,![]() ,
,
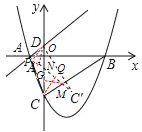
![]()
设![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
![]() ,即
,即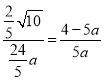 ,解得,
,解得,![]() (舍去),
(舍去),![]()
![]() ;
;
④当![]() 时,过M作
时,过M作![]() ,过点D作DP⊥MN于点P
,过点D作DP⊥MN于点P
![]()
设![]() ,则
,则![]()
![]()
![]()
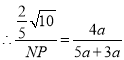
![]()
在![]() 中,
中,![]()
![]()
解得,![]() (舍去)
(舍去)
![]() .
.
综上,CM的长为![]() ,
,![]() ,
,![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,OE⊥BC垂足为E,AB⊥CD垂足为F.
(1)求证:AD=2OE;
(2)若∠ABC=30°,⊙O的半径为2,求两阴影部分面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
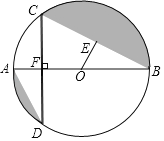
【题目】如图,在四边形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果点P由B点出发沿BC方向向点C匀速运动,同时点Q由A点出发沿AB方向向点B匀速运动,它们的速度均为1cm/s,当P点到达C点时,两点同时停止运动,连接PQ,设运动时间为t s,解答下列问题:
(1)当t为何值时,P,Q两点同时停止运动;
(2)设△PQB的面积为S,当t为何值时,S取得最大值,并求出最大值;
(3)当△PQB为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月15日,我国“两会”落下帷幕.13天时间里,来自各地的5000余名代表、委员聚于国家政治中心,共议国家发展大计.某校初三(3)班张老师为了了解同学们对“两会”知识的知晓情况,进行了一次小测试,测试满分100分.其中
A组同学的测试成绩分别为:91 91 86 93 85 89 89 88 87 91
B组同学的测试成绩分别为:88 97 88 85 86 94 84 83 98 87
根据以上数据,回答下列问题:
(1)完成下表:
组别 | 平均数 | 中位数 | 众数 | 方差 |
A组 | 89 | 89 | b | c |
B组 | 89 | a | 88 | 26.2 |
其中a= ,b= ,c= ,
(2)张老师将B组同学的测试成绩分成四组并绘制成如图所示频数分布直方图(不完整),请补全;
(3)根据以上分析,你认为 组(填“A”或“B”)的同学对今年“两会”知识的知晓情况更好一些,请写出你这样判断的理由(至少写两条):① ② .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间某商场搞促销活动,方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”、“20元”、“30元”、“50元”,顾客每消费满300元,就可从箱子里同时摸出两个球,根据这两个小球所标金额之和可获相应价格的礼品;
(1)若某顾客在甲商商场消费320元,至少可得价值______元的礼品,至多可得价值______元的礼品;
(2)请用画树状图或列表的方法,求该顾客去商场消费,获得礼品的总价值不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
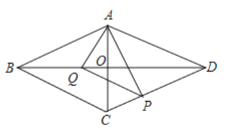
【题目】菱形![]() 中,对角线
中,对角线![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,运动速度都是
同时出发,运动速度都是![]() ,点
,点![]() 由
由![]() 向
向![]() 运动;点
运动;点![]() 由
由![]() 向
向![]() 运动,当
运动,当![]() 到达点
到达点![]() 时,
时,![]() ,
,![]() 两点运动停止,设时间为
两点运动停止,设时间为![]() 秒
秒![]() .连接
.连接![]() ,
,![]() ,
,![]() .
.
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)设![]() 的面积为
的面积为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() 的面积是四边形
的面积是四边形![]() 面积的
面积的![]() ;
;
(4)是否存在![]() 值,使得线段
值,使得线段![]() 经过
经过![]() 的中点
的中点![]() ;若存在,求出
;若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
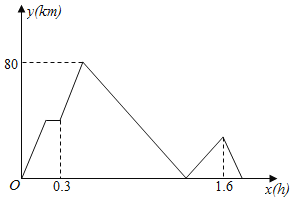
【题目】A,B两站相距330千米,甲、乙两车都从A站出发开往B站,甲车先出发,且在途中C站停靠6分钟,甲车出发半小时后,乙车从A站直达B站后停止,两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数图象如图,则乙车恰好追上甲车时距离C站有______千米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com