练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在Rt△ABC中，∠C=90°，若AB=
    		5
    ，BC=2，则sinB的值为（　　）
    A、
    		5
    5
    B、
    2
    		5
    5
    C、
    1
    2
    D、2
    考点：锐角三角函数的定义,勾股定理
    专题：
    分析：首先根据勾股定理求得AC的长，然后根据正弦函数的定义即可求解．
    解答：解：∵在Rt△ABC中，∠C=90°，AB=
    		5
    ，BC=2，
    ∴AC=
    		AB2-BC2
    =
    		(
    		5
    )2-22
    =1，
    ∴sinB=
    AC
    AB
    =
    1
    		5
    =
    		5
    5
    ．
    故选A．
    点评：本题主要考查了正弦函数的定义，正确记忆定义是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    下列合并同类项正确的是（　　）
    A、-5a3+2a3=-3
    B、ab+2ab=3a2b2
    C、0.75m2n-
    3
    4
    nm2=0
    D、4a2b-4ab=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，∠AOC与∠BOD是对顶角，OE平分∠AOC，OF平分∠BOD，求∠EOF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图所示，图（1）为一个长方体，AD=AB=10，AE=6，图2为图1的表面展开图（字在外表面上），请根据要求回答问题：

    （1）面“爱”的对面是面
     
    ；
    （2）如果面“丽”是右面，面“安”在后面，哪一面会在上面？
    （3）图（1）中，M，N为所在棱的中点，试在图（2）中画出点M，N的位置；并求出（2）中三角形ABM的面积．

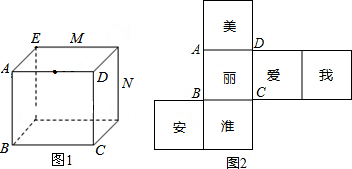
    查看答案和解析>>

    科目：初中数学 来源： 题型：

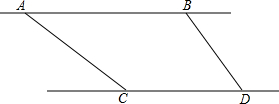    2014年3月8日凌晨，马来西亚航空公司MH370航班与总部失去联系，我国随即针对该航班展开了大规模搜救行动，我国的侦察机和搜救船在某海域同时沿同一方向配合搜寻（如图13）．在距海面900米的高空A处，侦察机测得搜救船在俯角为30°的海面C处，当侦察机以150
    		3
    米/分的速度平行海面飞行20分钟到达B处后，测得搜救船在俯角为60°的海面D处，求搜救船搜寻的平均速度．（结果保留整数，参考数据：
    		2
    ≈1.414，
    		3
    ≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，两个直角∠AOC和∠BOD有公共顶点O，下列结论：①∠AOB=∠COD；②∠AOB+∠COD=90°；③若OB平分∠AOC，则OC平分∠BOD；④∠AOD的平分线与∠BOC的平分线是同一条射线，其中正确的是
     
    ．（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，∠A+∠B=90°，点D在线段AB上，点E在线段AC上，DF平分∠BDE，DF与BC交于点F．
    （1）依题意补全图形；
    （2）若∠B+∠BDF=90°，求证：∠A=∠EDF．
    证明：∵∠A+∠B=90°，∠B+∠BDF=90°
    ∴
     
    （理由：
     
    ）
    又∵
     
    ．
    ∴∠BDF=∠EDF（理由：
     
    ）
    ∴∠A=∠EDF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    角度换算：42.13度=
     
    度
     
    分
     
    秒．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    满足-
    		3
    ＜x≤
    		5
    的整数x的和为
     
    ．

    查看答案和解析>>

    同步练习册答案