【题目】如图，△ABC中，∠C=90°，BC=7cm，AC=5，点P从B点出发，沿BC方向以2m/s的速度移动，点Q从C出发，沿CA方向以1m/s的速度移动．

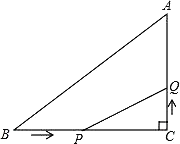
（1）若P、Q同时分别从B、C出发，那么几秒后，△PCQ的面积等于4？

（2）若P、Q同时分别从B、C出发，那么几秒后，PQ的长度等于5？

（3）△PCQ的面积何时最大，最大面积是多少？

参考答案：

【答案】（1）、秒；（2）秒；（3）当t=时△PCQ的面积最大，最大面积为．

【解析】

试题分析：（1）分别表示出线段CP和线段CQ的长，利用三角形的面积公式列出方程求解即可；

（2）表示出线段CP和CQ后利用勾股定理列出方程求解即可；

（3）列出△PCQ的面积关于t的函数解析式，配方可得最大值．

试题解析：（1）设t秒后△PCQ的面积等于4，根据题意得：CQ=t，BP=2t，则CP=7-2t，

CQ×CP=×t（7-2t）=4，

整理，得：t1=，t2=，

故若P、Q同时分别从B、C出发，那么、秒后，△PCQ的面积等于4；

（2）若PQ的长度等于5，则PC2+QC2=PQ2，

即：（7-2t）2+t2=25，

整理，得：5t2-28t+24=0，

解得：t1=，t2=，

∵CP=7-2t≥0，即t≤3.5，

∴t=＞3.5，舍去，

故那么秒后，PQ的长度等于5；

（3）由（1）知△PCQ的面积S=×t（7-2t）=-（t-）2+，

当t=时，S取得最大值，最大值为，

故当t=时△PCQ的面积最大，最大面积为．

关闭