
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
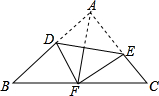 如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=$\frac{1}{2}$AB;②∠BAF=∠CAF;③S四边形ADFE=$\frac{1}{2}$S△ABC;④∠BDF+∠FEC=2∠BAC,正确的是④(把你认为正确的都填上,成立的说明理由).
如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF∥AB且EF=$\frac{1}{2}$AB;②∠BAF=∠CAF;③S四边形ADFE=$\frac{1}{2}$S△ABC;④∠BDF+∠FEC=2∠BAC,正确的是④(把你认为正确的都填上,成立的说明理由).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
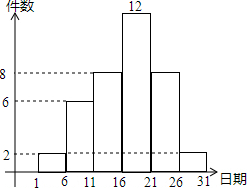 在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.
在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com