
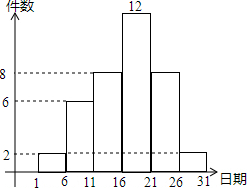
 在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.
在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.分析 (1)把各组的件数相加即可;
(2)根据所给频数分布直方图求出第2组和第4组的频数,然后分别求获奖率并比较;
(3)先求出该班在本次综合实践活动中作品未按时上交率,然后用样品估计总体即可.
解答 解:(1)本次活动作品总数=2+6+8+12+8+2=38件.
(2)第2组和第4组的频数分别为:6和12件,
第二组获奖率为:$\frac{4}{6}$=$\frac{2}{3}$,第四组获奖率为:$\frac{6}{12}$=$\frac{1}{2}$,
故第二组获奖率高.
(3)该班在本次综合实践活动中作品未按时上交率为:$\frac{40-38}{40}$=$\frac{1}{20}$,
故全校260名学生在本次综合实践活动中没有按时上交作品的学生个数为:500×$\frac{1}{20}$=25人.
点评 本题考查了频数分布直方图和用样本估计总体的知识,注意利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
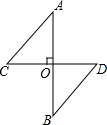 如图,AB⊥CD于O,且AO=BO,根据提示,添加一个条件使得Rt△AOC≌Rt△BOD.
如图,AB⊥CD于O,且AO=BO,根据提示,添加一个条件使得Rt△AOC≌Rt△BOD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
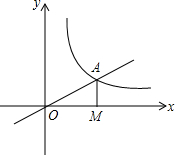 如图,正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.
如图,正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知△OAM的面积为1.如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
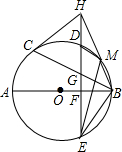 如图,AB、BC分别是⊙O的直径和弦,点D为$\widehat{BC}$上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD、ME、BE.求证:
如图,AB、BC分别是⊙O的直径和弦,点D为$\widehat{BC}$上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD、ME、BE.求证:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| A-C | C-D | E-D | E-F | G-F | B-G |
| 90m | 80m | 50 | -40m | -70m | 20m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com