
【题目】已知关于x的一元二次方程![]() 有两个实数根x1,x2.
有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得![]() 成立?若存在,请求出k的值;若不存在,请说明理由.
成立?若存在,请求出k的值;若不存在,请说明理由.
【答案】(1)![]() (2)不存在
(2)不存在
【解析】
(1)由题意可得△≥0,即[﹣(2k+1)]2﹣4(k2+2k)≥0,通过解该不等式即可求得k的取值范围;
(2)假设存在实数k使得x1·x2-x12-x22≥0成立.由根与系数的关系可得x1+x2=2k+1,x1·x2=k2+2k,然后利用完全平方公式可以把x1·x2-x12-x22≥0转化为3x1·x2-(x1+x2)2≥0的形式,通过解不等式可以求得k的值.
(1)∵原方程有两个实数根,
∴△≥0
即[﹣(2k+1)]2﹣4(k2+2k)≥0,
∴4k2+4k+1﹣4k2﹣8k≥0 ,
∴1﹣4k≥0,
∴k≤![]() ,
,
∴当k≤![]() 时,原方程有两个实数根;
时,原方程有两个实数根;
(2)假设存在实数k使得x1·x2-x12-x22≥0成立,
∵x1,x2是原方程的两根,
∴x1+x2=2k+1,x1·x2=k2+2k,
由x1·x2-x12-x22≥0,
得3x1·x2-(x1+x2)2≥0
∴3(k2+2k)﹣(2k+1)2≥0,
整理得:﹣(k﹣1)2≥0,
∴只有当k=1时,上式才能成立;
又∵由(1)知k≤![]() ,
,
∴不存在实数k使得x1·x2-x12-x22≥0成立.


科目:初中数学 来源: 题型:
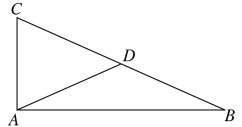
【题目】如图,在Rt△ABC中,∠BAC=90°,点D为BC中点,将△ABD绕点A按逆时针方向旋转50°,记点D在旋转过程中所经过的路径长为m,将△ABD绕点C按顺时针方向旋转100°,则点D在旋转过程中所经过的路径长为________.(用含m的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】聊城流传着一首家喻户晓的民谣:“东昌府,有三宝,铁塔、古楼、玉皇皋.”被人们誉为三宝之一的铁塔,初建年代在北宋早期,是本市现存最古老的建筑.如图,测绘师在离铁塔10米处的点C测得塔顶A的仰角为α,他又在离铁塔25米处的点D测得塔顶A的仰角为β,若tanαtanβ=1,点D,C,B在同一条直线上,那么测绘师测得铁塔的高度约为(参考数据: ![]() ≈3.162)( )
≈3.162)( )

A. 15.81米 B. 16.81米 C. 30.62米 D. 31.62米
查看答案和解析>>
科目:初中数学 来源: 题型:
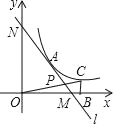
【题目】如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y=![]() (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l和反比例函数的解析式;
(2)在函数y=![]() (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com