
【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )

A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,![]() ,
,![]() ,点
,点![]() 是
是![]() 轴上点,点
轴上点,点![]() 为
为![]() 的中点.
的中点.
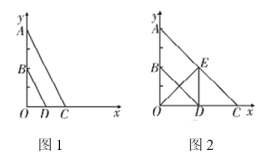
(1)求证:![]() ;
;
(2)若点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() 与
与![]() 的距离等于
的距离等于![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图2,若点![]() 在
在![]() 轴正半轴上,且
轴正半轴上,且![]() 于点
于点![]() ,当四边形
,当四边形![]() 为平行四边形时,求直线
为平行四边形时,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(每个学生必选且只能选一门课程)班主任想要了解全班同学对哪门课程感兴趣,就在全班进行调查,将获得的数据整理绘制成如图下所示两幅不完整的统计图.
学习感兴趣的课程情况条形统计图:

学习感兴趣的课程情况扇形统计图:
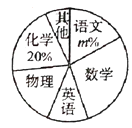
根据统计图信息,解答下列问题.
(1)全班共有________名学生,![]() 的值是________
的值是________
(2)据以上信息,补全条形统计图.
(3)扇形统计图中,“数学”所在扇形的圆心角是________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证:(1)EH=FH;
(2)∠CAB=2∠CDH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校七年级举行“每天锻炼一小时,健康生活一辈子”为主题的一分钟跳绳大赛,校团委组织了全级1000名学生参加为了解本次大赛的成绩,校团委随机抽取了其中100名学生的成绩(成绩取整数,总分100分)作为样本进行统计,制成如下不完整的统计图表根据所给信息,解答下列问题:
(1)m=______,n=_____.
(2)补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优”,请你估计该校七年级参加本次比赛的1000名学生中成绩是“优”的有多少人

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习新知:如图 1、图 2,![]() 是矩形
是矩形![]() 所在平面内任意一点,则有以下重要结论:
所在平面内任意一点,则有以下重要结论: ![]() .该结论的证明不难,同学们通过勾股定理即可证明.
.该结论的证明不难,同学们通过勾股定理即可证明.
应用新知:如图 3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 内一点,且
内一点,且![]() ,
,![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com