Question

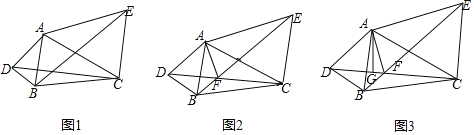
【题目】如图，△ABD和△ACE中，AB＝AD，AC＝AE，∠DAB＝∠CAE＝α，连接DC、BE．

（1）如图1，求证：DC＝BE；

（2）如图2，DC，BE交于点F，用含α的式子表示∠AFE；

（3）如图3，过A作AG⊥DC于点G，式于的值为　 　．

Answer 1

【答案】（1）证明见解析；（2）；（3）．

【解析】

（1）由∠DAB＝∠CAE＝α，可得∠DAC＝∠BAE，根据“SAS”可证△ADC≌△ABE，可得DC＝BE；

（2）由△ADC≌△ABE可得∠AEF＝∠ACD，即可证点A，点E，点C，点F四点共圆，可得∠AFE＝∠ACE，根据等腰三角形的性质和三角形内角和定理可求∠AFE的度数；

（3）由题意可得∠AFD＝＝∠AFE，过点作AH⊥BE，可证△AGF≌△AHF，可得AG＝AH，GF＝HF，即可证Rt△AGC≌Rt△AHE，可得GC＝HE，由EF﹣FC＝HE+FH﹣FC＝GC+FH﹣FC＝GF+FC+FH﹣FC＝2GF，可得的值．

（1）∵∠DAB＝∠CAE＝α，

∴∠DAB+∠BAC＝∠CAE+∠BAC

即∠DAC＝∠BAE，

又∵AD＝AB，AC＝AE

∴△ADC≌△ABE（SAS）

∴DC＝BE

（2）∵△ADC≌△ABE

∴∠AEF＝∠ACD

∴点A，点E，点C，点F四点共圆

∴∠AFE＝∠ACE

∵AC＝AE，∠DAB＝∠CAE＝α

∴∠ACE＝

∴∠AFE＝

（3）∵△ADC≌△ABE

∴∠ADC＝∠ABE

∴点A，点D，点B，点F四点共圆

∴∠AFD＝∠ABD

∵AB＝AD，∠DAB＝∠CAE＝α

∴∠ABD＝

∴∠AFD＝

∴∠AFE＝∠AFD

如图，过点作AH⊥BE，

∵∠AFE＝∠AFD，∠AGF＝∠AHF，AF＝AF

∴△AGF≌△AHF（AAS）

∴AG＝AH，GF＝HF，

∵AG＝AH，AE＝AC

∴Rt△AGC≌Rt△AHE（HL）

∴GC＝HE

∵EF﹣FC＝HE+FH﹣FC＝GC+FH﹣FC＝GF+FC+FH﹣FC＝2GF，

∴＝＝

故答案为：