
【题目】平面直角坐标系中,点A、B分别在x轴正半轴、y轴正半轴上,AO=BO,△ABO的面积为2.
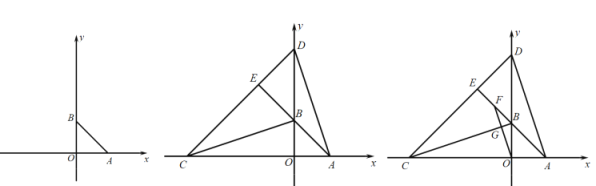
(1)求点A的坐标;
(2)点C、D分别在x轴负半轴、y轴正半轴上(D在B点上方),AD=BC,连接CD交AB延长线于E,设点E横坐标为t,△BCE的面积为S,求S与t的函数关系;
(3)在(2)的条件下,点F为BE中点,连接OF交BC于G,当∠CGO=90°时,求点D坐标.
【答案】(1)A(2,0);(2)S=t2-2t;(3)D(0,6).
【解析】
(1) 由△ABO的面积为2.得出方程,求出AO的长度,得出A的坐标;
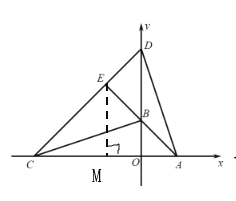
(2)过E作EM⊥AC于M,可证![]() ,可推出AC、EM、BO的长度,由
,可推出AC、EM、BO的长度,由![]() ,代入即可求出S与t的函数关系式.
,代入即可求出S与t的函数关系式.
(3)由∠CGO=90°可得BC⊥OF,然后根据![]() 列出方程求解即可.
列出方程求解即可.
解:(1)∵AO=BO,△ABO的面积为2.
∴![]()
∴AO=2
∴A(2,0)
(2)过E作EM⊥AC于M
∵∠AOB=90°,AO=BO
∴∠BAC=45°
∵∠AOD=∠BOC=90°
![]()
![]()
∴![]()
∴OC=OD
∵∠COD=90°,OC=OD
∴∠DCO=45°
∴∠BAC=∠DCO=45°
∴CE=EA,∠CEA=90°
∵EM⊥AC
∴M是AC的中点
∵点E横坐标为t
∴OM=|t|=-t
∴AM=2-t
∵∠CEA=90°, M是AC的中点
∴CM=EM=AM=2-t
∴AC=4-2t,OC=2-2t
∵![]()
∴![]()
=![]()
=![]()
=![]()
∴![]()
(3)∵OC=2-2t
∴C(2t-2,0)
∵B(0,2),C(2t-2,0)
∴![]()
∵EM =2-t
∴E(t, 2-t),
∵B(0.2), E(t, 2-t),点F为BE中点
∴F(![]() )
)
∵F(![]() ),O(0,0)
),O(0,0)
∴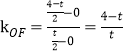
∵∠CGO=90°
∴BC⊥OF
∴![]()
∴![]()
解得:![]()
∵t<0
∴t=-2
∴OC=2-2t=2+4=6
∴OD=OC=6
∴D(0,6).


科目:初中数学 来源: 题型:
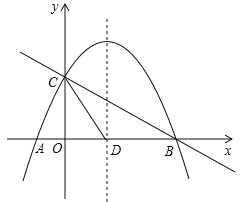
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,抛物线的对称轴交
轴交于点C,抛物线的对称轴交![]() 轴于点D,已知点A(-1,0),点C(0,2).
轴于点D,已知点A(-1,0),点C(0,2).
(1)求抛物线的函数解析式;
(2)线段BC上有一动点P,过点P作![]() 轴的平行线,交抛物线于点Q,求线段PQ的最大值;
轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)若点E在![]() 轴上,点F在抛物线上.是否存在以C、D、E、F为顶点且以CD为一边的平行四边形?若存在,请你求出点F的坐标;若不存在,请说明理由.
轴上,点F在抛物线上.是否存在以C、D、E、F为顶点且以CD为一边的平行四边形?若存在,请你求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)如图,Rt△ABC中,C= 90o,以斜边AB为边向外作正方形 ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6![]() ,则另一直角边BC的长为 ▲ .
,则另一直角边BC的长为 ▲ .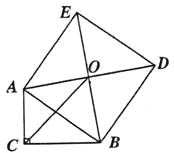
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在平行四边形![]() 内作一个菱形.甲,乙两位同学的作法分别如下:
内作一个菱形.甲,乙两位同学的作法分别如下:

对于甲乙两人的作法,可判断( )
A.甲正确,乙错误B.甲错误,乙正确C.甲,乙均正确D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮将笔记本电脑水平放置在桌子上,显示屏OA与底板OB所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架BCO'后,电脑转到B O′A′位置(如图3),侧面示意图为图4.已知OA=OB=28cm,O′C⊥OB于点C,O′C=14cm.
(参考数据:![]() ,
,![]() ,
,![]() )
)
(1)求∠CBO'的度数.
(2)显示屏的顶部A'比原来升高了多少cm?(结果精确到0.1cm)
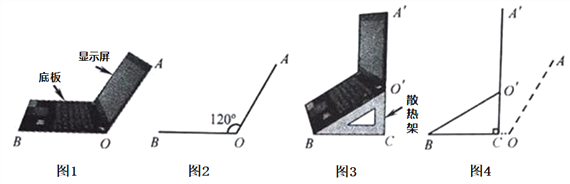
(3)如图4,垫入散热架后,要使显示屏O′A′与水平线的夹角仍保持120°,则显示屏O′A′应绕点O'按顺时针方向旋转多少度?(不写过程,只写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△OAB绕O点逆时针旋转60°得到△OCD,若OA=4,∠AOB=35°,则下列结论错误的是( )
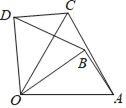
A. ∠BDO=60° B. ∠BOC=25° C. OC=4 D. BD=4
查看答案和解析>>
科目:初中数学 来源: 题型:
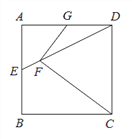
【题目】己知:如图,在正方形ABCD中,点E为边AB的中点,联结DE,点F在DE上CF=CD,过点F作FG⊥FC交AD于点G.
(1)求证:GF=GD;
(2)联结AF,求证:AF⊥DE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com