
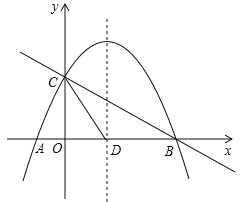
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,抛物线的对称轴交
轴交于点C,抛物线的对称轴交![]() 轴于点D,已知点A(-1,0),点C(0,2).
轴于点D,已知点A(-1,0),点C(0,2).
(1)求抛物线的函数解析式;
(2)线段BC上有一动点P,过点P作![]() 轴的平行线,交抛物线于点Q,求线段PQ的最大值;
轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)若点E在![]() 轴上,点F在抛物线上.是否存在以C、D、E、F为顶点且以CD为一边的平行四边形?若存在,请你求出点F的坐标;若不存在,请说明理由.
轴上,点F在抛物线上.是否存在以C、D、E、F为顶点且以CD为一边的平行四边形?若存在,请你求出点F的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当a=2时,PQ有最大值2;(3) 存在3个点符合题意,坐标分别是F1(
;(2)当a=2时,PQ有最大值2;(3) 存在3个点符合题意,坐标分别是F1(![]() )、F2(
)、F2(![]() )、F3(3,2).
)、F3(3,2).
【解析】分析:(1)将点A、C坐标代入求出函数解析式;
(2)先求出直线AB的函数解析式,然后设点P坐标为(a,b),并求出对应的点Q的坐标,然后求出线段PQ的最大值;
(3)本题应分情况讨论:
①将CD平移,令C点落在x轴(即E点)、D点落在抛物线(即F点)上,可根据平行四边形的性质,得出F点纵坐标,代入抛物线的解析式中即可求得F点坐标;
②过C作x轴的平行线,与抛物线的交点符合F点的要求,此时F、C的纵坐标相同,代入抛物线的解析式中即可求出F点坐标.
详解:(1)∵抛物线过点A(-1,0),C(0,2),
∴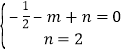 .解得
.解得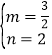 .
.
∴函数解析式为:![]() .
.
(2)由(1)得,![]() ,
,
令![]()
解得x=-1或x=4.∴A(-1,0)、B(4,0).
设直线BC解析式为y=kx+b,它过点B(4,0)、C(0,2),
则有![]() ,解得
,解得![]() .
.
∴直线BC解析式为![]() .
.
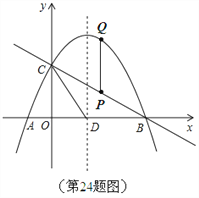
设点P横坐标为a,则点P纵坐标为![]() .
.
∵PQ∥y轴,
∴点Q的横坐标为a,纵坐标为![]() .
.
∴PQ=![]() -(
-(![]() )
)
=![]() =
=![]()
∵![]() ,∴其图象开口向下,有最大值.
,∴其图象开口向下,有最大值.
∴当a=2时,PQ有最大值2.
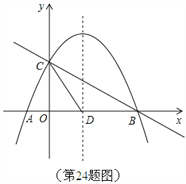
(3)如图所示.
①平移直线CD交x轴于点E,交x轴下方的抛物线于点F.
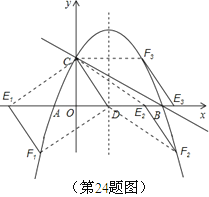
当CD=E1F1时,四边形CDEF为平行四边形.
∵C(0,2),∴设F(x,-2),
代入解析式得:![]() .
.
解得![]() .
.
此时存在点F1(![]() )、F2(
)、F2(![]() )
)
②过点C作CF3∥x轴交抛物线于点F3,过点F3作F3E3∥CD交x
轴于点E3,此时四边形CDE3F3为平行四边形.
此时F3纵坐标为2,将纵坐标代入函数解析式得
![]() .
.
解得:x=0或x=3.
此时存在点F3(3,2).
综上所述,存在3个点符合题意,坐标分别是F1(![]() )、F2(
)、F2(![]() )、F3(3,2).
)、F3(3,2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,各地采取价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过![]() 立方米时,水费按每立方米
立方米时,水费按每立方米![]() 元收费,超过
元收费,超过![]() 立方米时,不超过的部分每立方米仍按
立方米时,不超过的部分每立方米仍按![]() 元收费,超过的部分每立方米按
元收费,超过的部分每立方米按![]() 元收费,该市某户今年
元收费,该市某户今年![]() 月份的用水量和所交水费如下表所示:
月份的用水量和所交水费如下表所示:
月份 | 用水量( | 收费(元) |
|
|
|
|
|
|
设某户每月用水量![]() (立方米),应交水费
(立方米),应交水费![]() (元)
(元)
![]() 求
求![]() 的值,当
的值,当![]() 时,分别写出
时,分别写出![]() 与
与![]() 的函数关系式.
的函数关系式.
![]() 若该户
若该户![]() 月份用水量为
月份用水量为![]() 立方米,求该
立方米,求该![]() 月份水费多少元?
月份水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
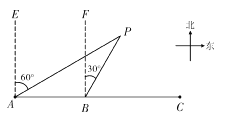
【题目】如图所示,C城市在A城市正东方向,现计划在A,C两城市间修建一条高速铁路(即线段AC),经测量,森林保护区的中心P在城市A的北偏东60°方向上,在线段AC上距A城市120 km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100 km为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于0.000 002 5 m的颗粒物,将0.000 002 5用科学记数法表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规律探究,观察下列等式:
第1个等式:![]()
第2个等式:![]()
第3个等式:![]()
第4个等式:![]()
请回答下列问题:
(1)按以上规律写出第5个等式:= ___________ = ___________
(2)用含n的式子表示第n个等式:= ___________ = ___________(n为正整数)
(3)求![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张和同学相约“五一”节到离家2400米的电影院看电影,到电影院后,发现电影票忘带了,此时离电影开始还有25分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回电影院,已知小张骑车的时间比跑步的时间少用了4分钟,骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度;
(2)如果小张在家取票和寻找“共享单车”共用了6分钟,他能否在电影开始前赶到电影院?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )

A. 40°B. 50°C. 60°D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究:哪些特殊的角可以用一副三角板画出?
在①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
(2)在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种.如图,他先用三角板画出了直线![]() ,然后将一副三角板拼接在一起,其中
,然后将一副三角板拼接在一起,其中![]() 角(
角(![]() )的顶点与
)的顶点与![]() 角(
角(![]() )的顶点互相重合,且边
)的顶点互相重合,且边![]() 、
、![]() 都在直线
都在直线![]() 上.固定三角板
上.固定三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 按顺时针方向旋转一个角度
按顺时针方向旋转一个角度![]() ,当边
,当边![]() 与射线
与射线![]() 第一次重合时停止.
第一次重合时停止.

①当![]() 平分
平分![]() 时,求旋转角度
时,求旋转角度![]() ;
;
②是否存在![]() ?若存在,求旋转角度
?若存在,求旋转角度![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点A、B分别在x轴正半轴、y轴正半轴上,AO=BO,△ABO的面积为2.
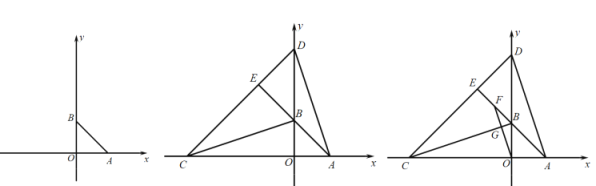
(1)求点A的坐标;
(2)点C、D分别在x轴负半轴、y轴正半轴上(D在B点上方),AD=BC,连接CD交AB延长线于E,设点E横坐标为t,△BCE的面积为S,求S与t的函数关系;
(3)在(2)的条件下,点F为BE中点,连接OF交BC于G,当∠CGO=90°时,求点D坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com