
【题目】为了加强公民的节水意识,合理利用水资源,各地采取价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过![]() 立方米时,水费按每立方米
立方米时,水费按每立方米![]() 元收费,超过
元收费,超过![]() 立方米时,不超过的部分每立方米仍按
立方米时,不超过的部分每立方米仍按![]() 元收费,超过的部分每立方米按
元收费,超过的部分每立方米按![]() 元收费,该市某户今年
元收费,该市某户今年![]() 月份的用水量和所交水费如下表所示:
月份的用水量和所交水费如下表所示:
月份 | 用水量( | 收费(元) |
|
|
|
|
|
|
设某户每月用水量![]() (立方米),应交水费
(立方米),应交水费![]() (元)
(元)
![]() 求
求![]() 的值,当
的值,当![]() 时,分别写出
时,分别写出![]() 与
与![]() 的函数关系式.
的函数关系式.
![]() 若该户
若该户![]() 月份用水量为
月份用水量为![]() 立方米,求该
立方米,求该![]() 月份水费多少元?
月份水费多少元?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解决问题:
(1)数学课上,老师提出如下问题:
观察下列算式:
![]() ;
;
![]() ;
;
![]()
![]()
![]()
…
若字母![]() 表示自然数,用含
表示自然数,用含![]() 的式子表示观察得到的规律是
的式子表示观察得到的规律是![]() ;
;
(2)小云同学解决完老师提出的问题后,又继续研究,发现:
①当![]() 表示负整数且
表示负整数且![]() 时,上述规律仍旧成立;
时,上述规律仍旧成立;
②当![]() 表示分数且
表示分数且![]() 时,上述规律仍旧成立.
时,上述规律仍旧成立.
请你对小云的两个发现进行验证,每个发现举出一个算式;
(3)请你参照小云同学的研究思路,进行猜想,验证、归纳,当![]() 时,
时,![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(4)进一步进行猜想、验证、归纳,当![]() (
(![]() 为有理数)时,
为有理数)时,![]() (用含
(用含![]() ,
,![]() ,
,![]() 的代数式表示)。
的代数式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂按用户的月需求量![]() (件)完成一种产品的生产,其中
(件)完成一种产品的生产,其中![]() .每件的售价为18万元,每件的成本
.每件的售价为18万元,每件的成本![]() (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量![]() (件)成反比.经市场调研发现,月需求量
(件)成反比.经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到了表中的数据.
为常数),且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 与
与![]() 满足的关系式,请说明一件产品的利润能否是12万元;
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求![]() ,并推断是否存在某个月既无盈利也不亏损;
,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第![]() 个月和第
个月和第![]() 个月的利润相差最大,求
个月的利润相差最大,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学科代表小芳对本年级同学参加课外兴趣小组活动情况进行随机抽样调查,根据调查数据小芳同学还制作了参加课外兴趣小组活动情况的两个统计图(见下图)
(1)此次被调查的人数是多少?
(2)将图②补充完整;
(3)求出图①中表示“写作”兴趣小组的扇形圆心角度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,顶点
,顶点![]() 是原点,顶点
是原点,顶点![]() 在
在![]() 轴上,顶点
轴上,顶点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 同时出发,以
同时出发,以![]() 的速度向点
的速度向点![]() 运动.规定其中一个动点到达端点时,另一个动点也随之停止运动;从运动开始,设
运动.规定其中一个动点到达端点时,另一个动点也随之停止运动;从运动开始,设![]() 点运动的时间为
点运动的时间为![]() .
.
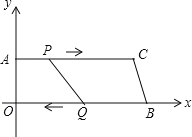
![]() 求直线
求直线![]() 的函数解析式;
的函数解析式;
![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 是矩形?
是矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形纸片ABCD的两边AB:BC=2:1,过点B折叠纸片,使点A落在边CD上的点F处,折痕为BE.若AB的长为4,则EF的长为( )
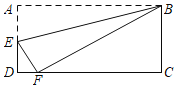
A. 8-4![]() B. 2
B. 2![]() C. 4
C. 4![]() 6D.
6D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是AC,BC上的点,且满足DE⊥EF,垂足为点E,连接DF.
(1)求∠EDF= (填度数);
(2)延长DE交AB于点G,连接FG,如图2,猜想AG,GF,FC三者的数量关系,并给出证明;
(3)①若AB=6,G是AB的中点,求△BFG的面积;
②设AG=a,CF=b,△BFG的面积记为S,试确定S与a,b的关系,并说明理由.
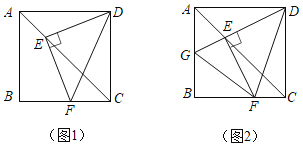
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,抛物线的对称轴交
轴交于点C,抛物线的对称轴交![]() 轴于点D,已知点A(-1,0),点C(0,2).
轴于点D,已知点A(-1,0),点C(0,2).
(1)求抛物线的函数解析式;
(2)线段BC上有一动点P,过点P作![]() 轴的平行线,交抛物线于点Q,求线段PQ的最大值;
轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)若点E在![]() 轴上,点F在抛物线上.是否存在以C、D、E、F为顶点且以CD为一边的平行四边形?若存在,请你求出点F的坐标;若不存在,请说明理由.
轴上,点F在抛物线上.是否存在以C、D、E、F为顶点且以CD为一边的平行四边形?若存在,请你求出点F的坐标;若不存在,请说明理由.
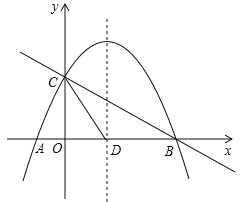
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com