
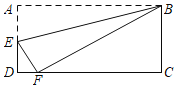
【题目】如图,已知矩形纸片ABCD的两边AB:BC=2:1,过点B折叠纸片,使点A落在边CD上的点F处,折痕为BE.若AB的长为4,则EF的长为( )
A. 8-4![]() B. 2
B. 2![]() C. 4
C. 4![]() 6D.
6D. ![]()
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
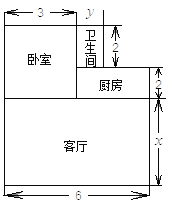
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(1)用含![]() 、
、![]() 的代数式表示地面总面积;
的代数式表示地面总面积;
(2)已知客厅面积比卫生间面积多21平方米,且地面总面积是卫生间面积的15倍.若铺1平方米地砖的平均费用为100元,那么铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,CE AB于E, CD平分ECB, 交过点B的射线于D, 交AB于F, 且BC=BD.
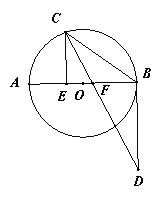
(1)求证:BD是⊙O的切线;
(2)若AE=9, CE=12, 求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,各地采取价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过![]() 立方米时,水费按每立方米
立方米时,水费按每立方米![]() 元收费,超过
元收费,超过![]() 立方米时,不超过的部分每立方米仍按
立方米时,不超过的部分每立方米仍按![]() 元收费,超过的部分每立方米按
元收费,超过的部分每立方米按![]() 元收费,该市某户今年
元收费,该市某户今年![]() 月份的用水量和所交水费如下表所示:
月份的用水量和所交水费如下表所示:
月份 | 用水量( | 收费(元) |
|
|
|
|
|
|
设某户每月用水量![]() (立方米),应交水费
(立方米),应交水费![]() (元)
(元)
![]() 求
求![]() 的值,当
的值,当![]() 时,分别写出
时,分别写出![]() 与
与![]() 的函数关系式.
的函数关系式.
![]() 若该户
若该户![]() 月份用水量为
月份用水量为![]() 立方米,求该
立方米,求该![]() 月份水费多少元?
月份水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
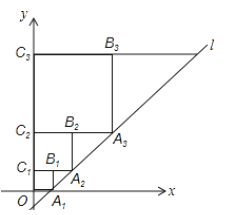
【题目】在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则点B2019的横坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,

(1)求证:AM=BN;
(2)写出点M在如图2所示位置时,线段AB、BM、BN三者之间的数量关系,并给出证明;
(3)点M在图3所示位置时,直接写出线段AB、BM、BN三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了解甲、乙两个部门员工的生产技能情况,从甲、乙两个部门各随机抽取20名员工,进行生产技能测试,测试成绩(百分制)如下:
甲7886 748175768770759075798170748086698377
乙9373 888172819483778380817081737882807040
(说明:成绩80分及以上为优秀,70-79分为良好,60-69分为合格,60分以下为不合格)
(1)请填完整表格:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 75 | |
乙 | 78 | 80.5 |
(2)从样本数据可以推断出 部门员工的生产技能水平较高,请说明理由.(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
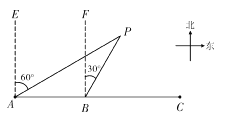
【题目】如图所示,C城市在A城市正东方向,现计划在A,C两城市间修建一条高速铁路(即线段AC),经测量,森林保护区的中心P在城市A的北偏东60°方向上,在线段AC上距A城市120 km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100 km为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )

A. 40°B. 50°C. 60°D. 70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com