
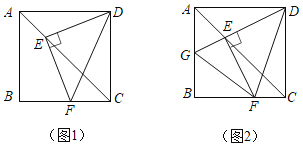
【题目】如图1,在正方形ABCD中,点E,F分别是AC,BC上的点,且满足DE⊥EF,垂足为点E,连接DF.
(1)求∠EDF= (填度数);
(2)延长DE交AB于点G,连接FG,如图2,猜想AG,GF,FC三者的数量关系,并给出证明;
(3)①若AB=6,G是AB的中点,求△BFG的面积;
②设AG=a,CF=b,△BFG的面积记为S,试确定S与a,b的关系,并说明理由.
【答案】(1)45°;(2)GF=AG+CF,证明见解析;(3)①6; ②![]() ,理由见解析.
,理由见解析.
【解析】
(1)如图1中,连接BE.利用全等三角形的性质证明EB=ED,再利用等角对等边证明EB=EF即可解决问题.
(2)猜想:GF=AG+CF.如图2中,将△CDF绕点D旋转90°,得△ADH,证明△GDH≌△GDF(SAS)即可解决问题.
(3)①设CF=x,则AH=x,BF=6-x,GF=3+x,利用勾股定理构建方程求出x即可.
②设正方形边长为x,利用勾股定理构建关系式,利用整体代入的思想解决问题即可.
解:(1)如图1中,连接BE.
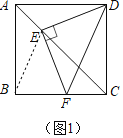
∵四边形ABCD是正方形,
∴CD=CB,∠ECD=∠ECB=45°,
∵EC=EC,
∴△ECB≌△ECD(SAS),
∴EB=ED,∠EBC=∠EDC,
∵∠DEF=∠DCF=90°,
∴∠EFC+∠EDC=180°,
∵∠EFB+∠EFC=180°,
∴∠EFB=∠EDC,
∴∠EBF=∠EFB,
∴EB=EF,
∴DE=EF,
∵∠DEF=90°,
∴∠EDF=45°
故答案为45°.
(2)猜想:GF=AG+CF.
如图2中,将△CDF绕点D旋转90°,得△ADH,
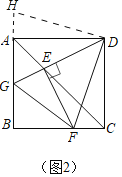
∴∠CDF=∠ADH,DF=DH,CF=AH,∠DAH=∠DCF=90°,
∵∠DAC=90°,
∴∠DAC+∠DAH=180°,
∴H、A、G三点共线,
∴GH=AG+AH=AG+CF,
∵∠EDF=45°,
∴∠CDF+∠ADG=45°,
∴∠ADH+∠ADG=45°
∴∠GDH=∠EDF=45°
又∵DG=DG
∴△GDH≌△GDF(SAS)
∴GH=GF,
∴GF=AG+CF.
(3)①设CF=x,则AH=x,BF=6-x,GF=3+x,
则有(3+x)2=(6-x)2+32,
解得x=2
∴S△BFG=![]() BFBG=6.
BFBG=6.
②设正方形边长为x,
∵AG=a,CF=b,
∴BF=x-b,BG=x-a,GF=a+b,
则有(x-a)2+(x-b)2=(a+b)2,
化简得到:x2-ax-bx=ab,
∴S=![]() (x-a)(x-b)=
(x-a)(x-b)=![]() (x2-ax-bx+ab)=
(x2-ax-bx+ab)=![]() ×2ab=ab.
×2ab=ab.


科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,各地采取价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过![]() 立方米时,水费按每立方米
立方米时,水费按每立方米![]() 元收费,超过
元收费,超过![]() 立方米时,不超过的部分每立方米仍按
立方米时,不超过的部分每立方米仍按![]() 元收费,超过的部分每立方米按
元收费,超过的部分每立方米按![]() 元收费,该市某户今年
元收费,该市某户今年![]() 月份的用水量和所交水费如下表所示:
月份的用水量和所交水费如下表所示:
月份 | 用水量( | 收费(元) |
|
|
|
|
|
|
设某户每月用水量![]() (立方米),应交水费
(立方米),应交水费![]() (元)
(元)
![]() 求
求![]() 的值,当
的值,当![]() 时,分别写出
时,分别写出![]() 与
与![]() 的函数关系式.
的函数关系式.
![]() 若该户
若该户![]() 月份用水量为
月份用水量为![]() 立方米,求该
立方米,求该![]() 月份水费多少元?
月份水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,

(1)求证:AM=BN;
(2)写出点M在如图2所示位置时,线段AB、BM、BN三者之间的数量关系,并给出证明;
(3)点M在图3所示位置时,直接写出线段AB、BM、BN三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了解甲、乙两个部门员工的生产技能情况,从甲、乙两个部门各随机抽取20名员工,进行生产技能测试,测试成绩(百分制)如下:
甲7886 748175768770759075798170748086698377
乙9373 888172819483778380817081737882807040
(说明:成绩80分及以上为优秀,70-79分为良好,60-69分为合格,60分以下为不合格)
(1)请填完整表格:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 75 | |
乙 | 78 | 80.5 |
(2)从样本数据可以推断出 部门员工的生产技能水平较高,请说明理由.(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣8)﹣(﹣15)+(﹣9)﹣(﹣12)
(2)7![]() +(﹣6.5)+3
+(﹣6.5)+3![]() +(﹣1.25)+2
+(﹣1.25)+2![]()
(3)(﹣81)÷(﹣2![]() )×
)×![]() ÷(﹣8)
÷(﹣8)
(4)![]()
(5)![]()
(6)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
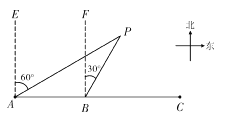
【题目】如图所示,C城市在A城市正东方向,现计划在A,C两城市间修建一条高速铁路(即线段AC),经测量,森林保护区的中心P在城市A的北偏东60°方向上,在线段AC上距A城市120 km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100 km为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于0.000 002 5 m的颗粒物,将0.000 002 5用科学记数法表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究:哪些特殊的角可以用一副三角板画出?
在①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
(2)在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种.如图,他先用三角板画出了直线![]() ,然后将一副三角板拼接在一起,其中
,然后将一副三角板拼接在一起,其中![]() 角(
角(![]() )的顶点与
)的顶点与![]() 角(
角(![]() )的顶点互相重合,且边
)的顶点互相重合,且边![]() 、
、![]() 都在直线
都在直线![]() 上.固定三角板
上.固定三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 按顺时针方向旋转一个角度
按顺时针方向旋转一个角度![]() ,当边
,当边![]() 与射线
与射线![]() 第一次重合时停止.
第一次重合时停止.

①当![]() 平分
平分![]() 时,求旋转角度
时,求旋转角度![]() ;
;
②是否存在![]() ?若存在,求旋转角度
?若存在,求旋转角度![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com