
【题目】在矩形ABCD中,点A关于∠B的平分线的对称点为E,点E关于∠C的平分线的对称点为F.若AD=![]() AB=2
AB=2![]() ,则AF2=_____.
,则AF2=_____.
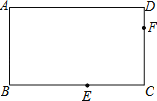
【答案】40﹣16![]()
【解析】
由AD=![]() AB=2
AB=2![]() ,可求得AB=2,AD=2
,可求得AB=2,AD=2![]() ,又由在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F,根据轴对称的性质,可求得BE,CF的长,继而求得DF的长,然后由勾股定理求得答案.
,又由在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F,根据轴对称的性质,可求得BE,CF的长,继而求得DF的长,然后由勾股定理求得答案.
∵AD=![]() AB=2
AB=2![]() ,
,
∴AB=2,AD=2![]() ,
,
∵四边形ABCD是矩形,
∴BC=AD=2![]() ,CD=AB=2,
,CD=AB=2,
∵在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F,
∴BE=AB=2,
∴CF=CE=BC﹣BE=2![]() ﹣2,
﹣2,
∴DF=CD﹣CF=4﹣2![]() ,
,
∴AF2=AD2+DF2=(2![]() )2+(4﹣2
)2+(4﹣2![]() )2=40﹣16
)2=40﹣16![]() .
.
故答案为:40﹣16![]() ;
;


科目:初中数学 来源: 题型:
【题目】某市在艺术节中组织中小学校文艺汇演,甲、乙两所学校共92名学生![]() 其中甲校学生多于乙校学生,且甲校学生不足90名
其中甲校学生多于乙校学生,且甲校学生不足90名![]() ,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两所学校单独购买服装,一共应付5000元
(1)甲、乙两校各有多少名学生准备参加汇演?
(2)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(3)如果甲校有10名学生被调去参加书法绘画比赛不能参加演出,请你为两校设计购买服装方案,并说明哪一种最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若BC=4,BG=3,则GE的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案;在甲超市累计购买商品超出200元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出100元之后,超出部分按原价8.5折优惠,设顾客购物的原费用是x元(x>200).
(1)请用含x的代数式分别表示顾客在两家超市购物所付的实际费用;
(2)李明慧准备购买300元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明慧购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,D为BC的中点,连接AD,E为AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF为平行四边形.
(2)当四边形ADCF为矩形时,AB与AC应满足怎样的数量关系?请说明理由.
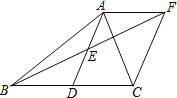
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解决问题:
(1)数学课上,老师提出如下问题:
观察下列算式:
![]() ;
;
![]() ;
;
![]()
![]()
![]()
…
若字母![]() 表示自然数,用含
表示自然数,用含![]() 的式子表示观察得到的规律是
的式子表示观察得到的规律是![]() ;
;
(2)小云同学解决完老师提出的问题后,又继续研究,发现:
①当![]() 表示负整数且
表示负整数且![]() 时,上述规律仍旧成立;
时,上述规律仍旧成立;
②当![]() 表示分数且
表示分数且![]() 时,上述规律仍旧成立.
时,上述规律仍旧成立.
请你对小云的两个发现进行验证,每个发现举出一个算式;
(3)请你参照小云同学的研究思路,进行猜想,验证、归纳,当![]() 时,
时,![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(4)进一步进行猜想、验证、归纳,当![]() (
(![]() 为有理数)时,
为有理数)时,![]() (用含
(用含![]() ,
,![]() ,
,![]() 的代数式表示)。
的代数式表示)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂按用户的月需求量![]() (件)完成一种产品的生产,其中
(件)完成一种产品的生产,其中![]() .每件的售价为18万元,每件的成本
.每件的售价为18万元,每件的成本![]() (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量![]() (件)成反比.经市场调研发现,月需求量
(件)成反比.经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到了表中的数据.
为常数),且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 与
与![]() 满足的关系式,请说明一件产品的利润能否是12万元;
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求![]() ,并推断是否存在某个月既无盈利也不亏损;
,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第![]() 个月和第
个月和第![]() 个月的利润相差最大,求
个月的利润相差最大,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是AC,BC上的点,且满足DE⊥EF,垂足为点E,连接DF.
(1)求∠EDF= (填度数);
(2)延长DE交AB于点G,连接FG,如图2,猜想AG,GF,FC三者的数量关系,并给出证明;
(3)①若AB=6,G是AB的中点,求△BFG的面积;
②设AG=a,CF=b,△BFG的面积记为S,试确定S与a,b的关系,并说明理由.
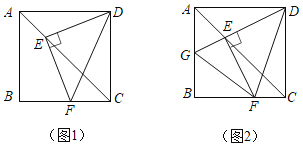
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com