Question

【题目】某厂按用户的月需求量(件)完成一种产品的生产，其中．每件的售价为18万元，每件的成本(万元)是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量(件)成反比．经市场调研发现，月需求量与月份(为整数，)符合关系式(为常数)，且得到了表中的数据．

月份(月)	1	2
成本(万元/件)	11	12
需求量(件/月)	120	100

(1)求与满足的关系式，请说明一件产品的利润能否是12万元；

(2)求，并推断是否存在某个月既无盈利也不亏损；

(3)在这一年12个月中，若第个月和第个月的利润相差最大，求．

Answer 1

【答案】(1)，不可能；(2)不存在；(3)1或11.

【解析】

试题分析：(1)根据每件的成本y(万元)是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量x(件)成反比，结合表格，用待定系数法求y与x之间的函数关系式，再列方程求解，检验所得结果是还符合题意；(2)将表格中的n，对应的x值，代入到，求出k，根据某个月既无盈利也不亏损，得到一个关于n的一元二次方程，判断根的情况；(3)用含m的代数式表示出第m个月，第(m+1)个月的利润，再对它们的差的情况讨论.

试题解析：(1)由题意设，由表中数据，得

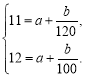解得∴.

由题意，若，则.

∵x＞0，∴.

∴不可能.

(2)将n=1，x=120代入，得

120=2-2k+9k+27.解得k=13.

将n=2，x=100代入也符合.

∴k=13.

由题意，得18=6+，求得x=50.

∴50=，即.

∵，∴方程无实数根.

∴不存在.

(3)第m个月的利润为w==；

∴第(m+1)个月的利润为

W′=.

若W≥W′，W-W′=48(6-m),m取最小1，W-W′=240最大.

若W＜W′，W′-W=48(m-6),m+1≤12，m取最大11，W′-W=240最大.

∴m=1或11.