
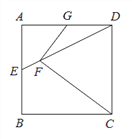
【题目】己知:如图,在正方形ABCD中,点E为边AB的中点,联结DE,点F在DE上CF=CD,过点F作FG⊥FC交AD于点G.
(1)求证:GF=GD;
(2)联结AF,求证:AF⊥DE.
【答案】(1)证明见解析(2)证明见解析
【解析】分析:![]() 根据等角的余角相等得到
根据等角的余角相等得到![]() 即可证明.
即可证明.
![]() 联结CG.证明△DAE≌△CDG,得到
联结CG.证明△DAE≌△CDG,得到![]() .进而得到
.进而得到![]() ,根据等边对等角得到
,根据等边对等角得到![]() 根据三角形的内角和可以求出∠AFD= 90°,即可证明.
根据三角形的内角和可以求出∠AFD= 90°,即可证明.
详解:∵四边形![]() 是正方形,∴
是正方形,∴![]() ,
,
∵FG⊥FC, ∴∠GFC= 90°,
∵![]() ∴∠CDF=∠CFD ,
∴∠CDF=∠CFD ,
∴∠GFC-∠CFD=∠ADC-∠CDE,即∠GFD=∠GDF.
∴GF=GD.
![]() 联结CG.
联结CG.
∵![]() ∴点
∴点![]() 在线段
在线段![]() 的中垂线上,
的中垂线上,
∴GC⊥DE,
∴∠CDF+∠DCG= 90°,
∵∠CDF+∠ADE= 90°,
∴∠DCG=∠ADE.
四边形![]() 是正方形,
是正方形,
∴AD=DC,∠DAE=∠CDG= 90°,
∴△DAE≌△CDG,
∴![]() .
.
点![]() 是边
是边![]() 的中点,
的中点,
![]() 点
点![]() 是边
是边![]() 的中点,
的中点,
∴![]() ,
,
∴![]()
∵![]()
∴![]()
∴∠AFD= 90°,即AF⊥DE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点A、B分别在x轴正半轴、y轴正半轴上,AO=BO,△ABO的面积为2.
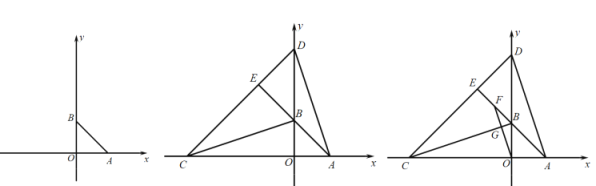
(1)求点A的坐标;
(2)点C、D分别在x轴负半轴、y轴正半轴上(D在B点上方),AD=BC,连接CD交AB延长线于E,设点E横坐标为t,△BCE的面积为S,求S与t的函数关系;
(3)在(2)的条件下,点F为BE中点,连接OF交BC于G,当∠CGO=90°时,求点D坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了进一步改进本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.

请你根据以上提供的信息,解答下列问题:
(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是 ;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是直角三角形,其中
是直角三角形,其中![]() .
.
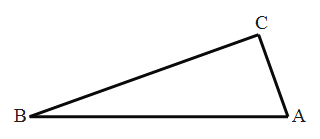
(1)画出![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 后的
后的![]() ;
;
(2)线段![]() 在旋转过程中所扫过部分的周长是_________(保留
在旋转过程中所扫过部分的周长是_________(保留![]() );
);
(3)求线段![]() 在旋转过程中所扫过部分的面积(结果保留
在旋转过程中所扫过部分的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
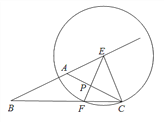
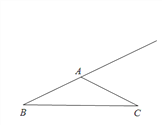
【题目】如图,己知在△ABC中,AB=AC,tanB=![]() ,BC =4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.
,BC =4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.
(1)求证:AE2=AP·AC;
(2)当点F在线段BC上,设CF=x,△PFC的面积为y,求y关于x的函数解析式及定义域;
(3)当![]() 时,求BE的长.
时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
①![]()
②![]()
③![]()
④![]()
(1)请你紧接着写出两个等式:
⑤_____________;
⑥_____________;
(2)根据以上式子的规律,请你写出第![]() 个式子.
个式子.
(3)利用这个规律计算:![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
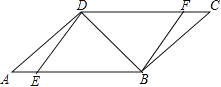
【题目】(2015南通)如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
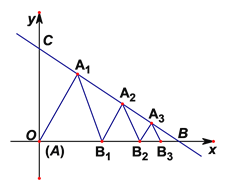
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .在
.在![]() 内依次作等边三角形使一边在
内依次作等边三角形使一边在![]() 轴上,另一个顶点在
轴上,另一个顶点在![]() 边上,作出的等边三角形第一个是
边上,作出的等边三角形第一个是![]() ,第二个是
,第二个是![]() ,第三个是
,第三个是![]() …
…
(1)![]() 的边长等于________;
的边长等于________;
(2)![]() 的边长等于________.
的边长等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com