
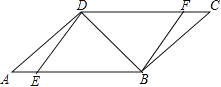
【题目】(2015南通)如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.
【答案】答案见解析.
【解析】试题分析:(1)由平行四边形的性质得到对边平行且相等,对角相等,再由垂直的定义得到一对直角相等,利用等式的性质等到一对角相等,利用ASA即可得证;
(2)过点D作DH⊥AB,在Rt△ADH中,有AD=2DH,在Rt△DEB中,有EB=2DH,易得四边形EBFD为平行四边形,利用平行四边形的对边相等得到EB=DF,等量代换即可得证.
试题解析:(1)∵四边形ABCD是平行四边形,∴AD=CB,∠A=∠C,AD//CB,
∴∠ADB=∠CBD,
∵ED⊥DB,FB⊥BD,∴∠EDB=∠FBD=90°,∴∠ADE=∠CBF,
在△AED和△CFB中,∠ADE=∠CBD,AD=BC,∠A=∠C,∴△AED≌△CFB(ASA);
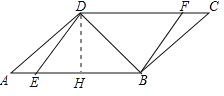
(2)作DH⊥AB,垂足为H,
在R t△ADH在,∠A=30°,∴AD=2DH,
在Rt△DEB中,∠DEB=45°,∴EB=2DH,
∵∠EDB=∠FBD=90°,∴DE//BF,又∵DC//AB,∴四边形DEBF是平行四边形,
∴FD=BE,∴DA=DF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将△OAB绕O点逆时针旋转60°得到△OCD,若OA=4,∠AOB=35°,则下列结论错误的是( )
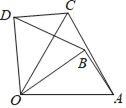
A. ∠BDO=60° B. ∠BOC=25° C. OC=4 D. BD=4
查看答案和解析>>
科目:初中数学 来源: 题型:
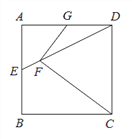
【题目】己知:如图,在正方形ABCD中,点E为边AB的中点,联结DE,点F在DE上CF=CD,过点F作FG⊥FC交AD于点G.
(1)求证:GF=GD;
(2)联结AF,求证:AF⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
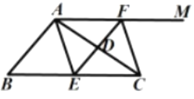
【题目】如图,AM∥BC,D,E分别为AC,BC的中点,射线ED交AM于点F,连接AE,CF。
(1)求证:四边形ABEF是平行四边形;
(2)当AB=AC时,求证:四边形AECF时矩形;
(3)当∠BAC=90°时,判断四边形AECF的形状,(只写结论,不必证明)。
查看答案和解析>>
科目:初中数学 来源: 题型:
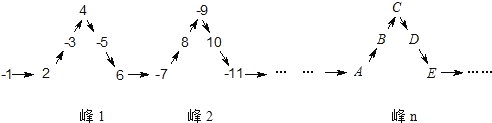
【题目】将一列有理数-1,2,-3,4,-5,6,…如图所示排列,根据图中的排列规律可知,“峰1”中封顶的位置(![]() 的位置)是有理数4,“峰2”中封顶的位置(
的位置)是有理数4,“峰2”中封顶的位置(![]() 的位置)是有理数-9,按此规律排列,2020应排在
的位置)是有理数-9,按此规律排列,2020应排在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中________的位置.
中________的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为6cm,点E,M分别是线段BD,AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图①,若点M与点D重合,求证:AF=MN;
(2)如图②,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以![]() cm/s的速度沿BD向点D运动,运动时间为ts.
cm/s的速度沿BD向点D运动,运动时间为ts.
①设BF=ycm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直接写出结果:
(1)﹣1+2=_____;
(2)﹣1﹣1=_____;
(3)(﹣3)3=_____;
(4)6÷(﹣1![]() )=_____;
)=_____;
(5)(﹣1)2n﹣(﹣1)2n﹣1=_____(n为正整数);
(6)方程4x=0的解为_____;
(7)方程﹣![]() x=2的解为_____.
x=2的解为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
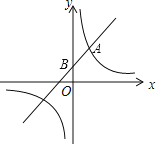
【题目】如图,一次函数y=kx+b(k≠0)经过点B(0,1),且与反比例函数y=![]() (m≠0)的图象在第一象限有公共点A(1,2).
(m≠0)的图象在第一象限有公共点A(1,2).
(1)求一次函数与反比例函数的解析式;
(2)根据图象写出当x取何值时,一次函数的值小于反比例函数的值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com