
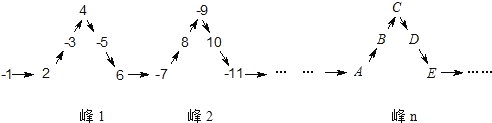
【题目】将一列有理数-1,2,-3,4,-5,6,…如图所示排列,根据图中的排列规律可知,“峰1”中封顶的位置(![]() 的位置)是有理数4,“峰2”中封顶的位置(
的位置)是有理数4,“峰2”中封顶的位置(![]() 的位置)是有理数-9,按此规律排列,2020应排在
的位置)是有理数-9,按此规律排列,2020应排在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中________的位置.
中________的位置.
【答案】![]()
【解析】
观察题中数列的规律:奇数前面是负号,偶数前面是正(省略),峰n中,A位置的绝对值可以表示为:5n-3;B位置的绝对值可以表示为:5n-2;C位置的绝对值可以表示为:5n-1;D位置的绝对值可以表示为:5n;E位置的绝对值可以表示为:5n+1;注意先判断绝对值的位置再判断符号,根据规律求解即可.
观察发现:峰n中,A位置的绝对值可以表示为:5n-3;
B位置的绝对值可以表示为:5n-2;
C位置(峰顶)的绝对值可以表示为:5n-1;
D位置的绝对值可以表示为:5n;
E位置的绝对值可以表示为:5n+1;
根据规律,|-2020|=2020,2020÷5=404,是5的倍数,
∴2020应排在D的位置.
故答案:D.


科目:初中数学 来源: 题型:
【题目】由![]() 个完全相同的小正方体搭成的物体如图所示.
个完全相同的小正方体搭成的物体如图所示.
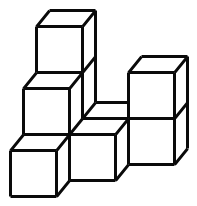
(1)请在下面的方格图中画出该物体的主视图和左视图;
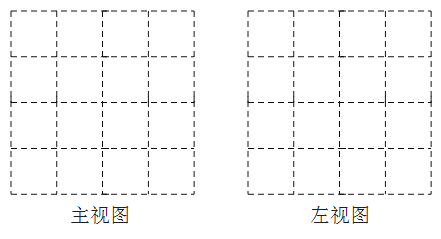
(2)如果再添加若干个相同的小正方体之后,所得到的新物体的主视图和左视图跟原来的相间,那么这样的小正方体最多还可以添加 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
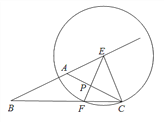
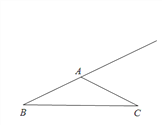
【题目】如图,己知在△ABC中,AB=AC,tanB=![]() ,BC =4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.
,BC =4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.
(1)求证:AE2=AP·AC;
(2)当点F在线段BC上,设CF=x,△PFC的面积为y,求y关于x的函数解析式及定义域;
(3)当![]() 时,求BE的长.
时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
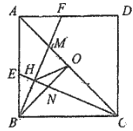
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
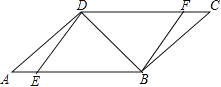
【题目】(2015南通)如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
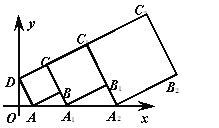
【题目】在平面坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2018个正方形的面积为( )
A. 5·![]() B. 5·
B. 5·![]() C. 5·
C. 5·![]() D. 5·
D. 5·![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
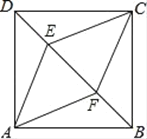
【题目】如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.
(1)判断四边形AECF是什么特殊四边形,并证明;
(2)若EF=4,DE=BF=2,求四边形AECF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
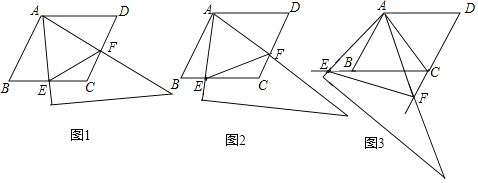
【题目】已知:四边形ABCD是菱形,AB=4,∠ABC=60°,有一足够大的含60°角的直角三角尺的60°角的顶点与菱形ABCD的顶点A重合,两边分别射线CB、DC相交于点E、F,且∠EAP=60°.
(1)如图1,当点E是线段CB的中点时,请直接判断△AEF的形状是 .
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com