
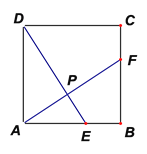
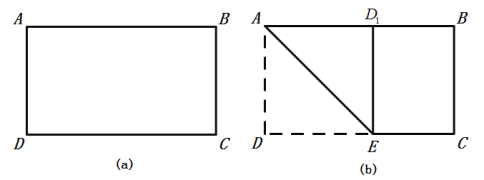
ЁОЬтФПЁПвбжЊЃКЫФБпаЮABCDЪЧСтаЮЃЌABЃН4ЃЌЁЯABCЃН60ЁуЃЌгавЛзуЙЛДѓЕФКЌ60ЁуНЧЕФжБНЧШ§НЧГпЕФ60ЁуНЧЕФЖЅЕугыСтаЮABCDЕФЖЅЕуAжиКЯЃЌСНБпЗжБ№ЩфЯпCBЁЂDCЯрНЛгкЕуEЁЂFЃЌЧвЁЯEAPЃН60ЁуЃЎ
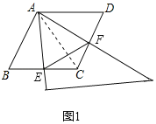
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуEЪЧЯпЖЮCBЕФжаЕуЪБЃЌЧыжБНгХаЖЯЁїAEFЕФаЮзДЪЧЁЁ ЁЁЃЎ
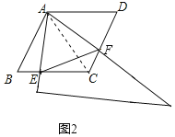
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуEЪЧЯпЖЮCBЩЯШЮвтвЛЕуЪБЃЈЕуEВЛгыBЁЂCжиКЯЃЉЃЌЧѓжЄЃКBEЃНCFЃЛ
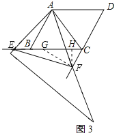
ЃЈ3ЃЉШчЭМ3ЃЌЕБЕуEдкЯпЖЮCBЕФбгГЄЯпЩЯЃЌЧвЁЯEABЃН15ЁуЪБЃЌЧѓЕуFЕНBCЕФОрРыЃЎ
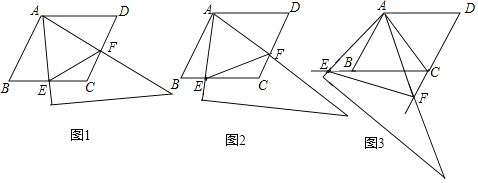
ЁОД№АИЁПЃЈ1ЃЉЁїAEFЪЧЕШБпШ§НЧаЮЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉЕуFЕНBCЕФОрРыЮЊ3Љ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉСЌНгACЃЌжЄУїЁїABCЪЧЕШБпШ§НЧаЮЃЌЕУГіACЃНABЃЌдйжЄУїЁїBAEЁеЁїDAFЃЌЕУГіAEЃНAFЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉСЌНгACЃЌЭЌЃЈ1ЃЉЕУЃКЁїABCЪЧЕШБпШ§НЧаЮЃЌЕУГіЁЯBACЃНЁЯACBЃН60ЁуЃЌABЃНACЃЌдйжЄУїЁїBAEЁеЁїCAFЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЭЌЃЈ1ЃЉЕУЃКЁїABCКЭЁїACDЪЧЕШБпШ§НЧаЮЃЌЕУГіABЃНACЃЌЁЯBACЃНЁЯACBЃНЁЯACDЃН60ЁуЃЌжЄУїЁїBAEЁеЁїCAFЃЌЕУГіBEЃНCFЃЌAEЃНAFЃЌжЄГіЁїAEFЪЧЕШБпШ§НЧаЮЃЌЕУГіЁЯAEFЃН60ЁуЃЌжЄГіЁЯAEBЃН45ЁуЃЌЕУГіЁЯCEFЃНЁЯAEFЉЁЯAEBЃН15ЁуЃЌзїFHЁЭBCгкHЃЌдкЁїCEFФкВПзїЁЯEFGЃНЁЯCEFЃН15ЁуЃЌдђGEЃНGFЃЌЁЯFGHЃН30ЁуЃЌгЩжБНЧШ§НЧаЮЕФаджЪЕУГіFGЃН2FHЃЌGHЃН![]() FHЃЌCFЃН2CHЃЌFHЃН
FHЃЌCFЃН2CHЃЌFHЃН![]() CHЃЌЩшCHЃНxЃЌдђBEЃНCFЃН2xЃЌFHЃН
CHЃЌЩшCHЃНxЃЌдђBEЃНCFЃН2xЃЌFHЃН![]() xЃЌGEЃНGFЃН2FHЃН2
xЃЌGEЃНGFЃН2FHЃН2![]() xЃЌGHЃН
xЃЌGHЃН![]() FHЃН3xЃЌЕУГіEHЃН4+xЃН2
FHЃН3xЃЌЕУГіEHЃН4+xЃН2![]() x+3xЃЌНтЕУЃКxЃН
x+3xЃЌНтЕУЃКxЃН![]() Љ1ЃЌЧѓГіFHЃН
Љ1ЃЌЧѓГіFHЃН![]() xЃН3Љ
xЃН3Љ![]() МДПЩЃЎ
МДПЩЃЎ
ЃЈ1ЃЉНтЃКЁїAEFЪЧЕШБпШ§НЧаЮЃЌРэгЩШчЯТЃК
СЌНгACЃЌШчЭМ1ЫљЪОЃК
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрABЃНBCЃНADЃЌЁЯBЃНЁЯDЃЌ
ЁпЁЯABCЃН60ЁуЃЌ
ЁрЁЯBADЃН120ЁуЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрACЃНABЃЌ
ЁпЕуEЪЧЯпЖЮCBЕФжаЕуЃЌ
ЁрAEЁЭBCЃЌ
ЁрЁЯBAEЃН30ЁуЃЌ
ЁпЁЯEAFЃН60ЁуЃЌ
ЁрЁЯDAFЃН120ЁуЉ30ЁуЉ60ЁуЃН30ЁуЃНЁЯBAEЃЌ
дкЁїBAEКЭЁїDAFжаЃЌ
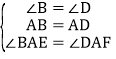 ЃЌ
ЃЌ
ЁрЁїBAEЁеЁїDAFЃЈASAЃЉЃЌ
ЁрAEЃНAFЃЌ
гжЁпЁЯEAFЃН60ЁуЃЌ
ЁрЁїAEFЪЧЕШБпШ§НЧаЮЃЛ
ЙЪД№АИЮЊЃКЕШБпШ§НЧаЮЃЛ
ЃЈ2ЃЉжЄУїЃКСЌНгACЃЌШчЭМ2ЫљЪОЃК
ЭЌЃЈ1ЃЉЕУЃКЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯBACЃНЁЯACBЃН60ЁуЃЌABЃНACЃЌ
ЁпЁЯEAFЃН60ЁуЃЌ
ЁрЁЯBAEЃНЁЯCAFЃЌ
ЁпЁЯBCDЃНЁЯBADЃН120ЁуЃЌ
ЁрЁЯACFЃН60ЁуЃНЁЯBЃЌ
дкЁїBAEКЭЁїCAFжаЃЌ
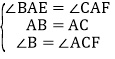 ЃЌ
ЃЌ
ЁрЁїBAEЁеЁїCAFЃЈASAЃЉЃЌ
ЁрBEЃНCFЃЛ
ЃЈ3ЃЉНтЃКЭЌЃЈ1ЃЉЕУЃКЁїABCКЭЁїACDЪЧЕШБпШ§НЧаЮЃЌ
ЁрABЃНACЃЌЁЯBACЃНЁЯACBЃНЁЯACDЃН60ЁуЃЌ
ЁрЁЯACFЃН120ЁуЃЌ
ЁпЁЯABCЃН60ЁуЃЌ
ЁрЁЯABEЃН120ЁуЃНЁЯACFЃЌ
ЁпЁЯEAFЃН60ЁуЃЌ
ЁрЁЯBAEЃНЁЯCAFЃЌ
дкЁїBAEКЭЁїCAFжаЃЌ
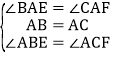 ЃЌ
ЃЌ
ЁрЁїBAEЁеЁїCAFЃЈASAЃЉЃЌ
ЁрBEЃНCFЃЌAEЃНAFЃЌ
ЁпЁЯEAFЃН60ЁуЃЌ
ЁрЁїAEFЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯAEFЃН60ЁуЃЌ
ЁпЁЯEABЃН15ЁуЃЌЁЯABCЃНЁЯAEB+ЁЯEABЃН60ЁуЃЌ
ЁрЁЯAEBЃН45ЁуЃЌ
ЁрЁЯCEFЃНЁЯAEFЉЁЯAEBЃН15ЁуЃЌ
зїFHЁЭBCгкHЃЌдкЁїCEFФкВПзїЁЯEFGЃНЁЯCEFЃН15ЁуЃЌШчЭМ3ЫљЪОЃК
дђGEЃНGFЃЌЁЯFGHЃН30ЁуЃЌ
ЁрFGЃН2FHЃЌGHЃН![]() FHЃЌ
FHЃЌ
ЁпЁЯFCHЃНЁЯACFЉЁЯACBЃН60ЁуЃЌ
ЁрЁЯCFHЃН30ЁуЃЌ
ЁрCFЃН2CHЃЌFHЃН![]() CHЃЌ
CHЃЌ
ЩшCHЃНxЃЌдђBEЃНCFЃН2xЃЌFHЃН![]() xЃЌGEЃНGFЃН2FHЃН2
xЃЌGEЃНGFЃН2FHЃН2![]() xЃЌGHЃН
xЃЌGHЃН![]() FHЃН3xЃЌ
FHЃН3xЃЌ
ЁпBCЃНABЃН4ЃЌ
ЁрCEЃНBC+BEЃН4+2xЃЌ
ЁрEHЃН4+xЃН2![]() x+3xЃЌ
x+3xЃЌ
НтЕУЃКxЃН![]() Љ1ЃЌ
Љ1ЃЌ
ЁрFHЃН![]() xЃН3Љ
xЃН3Љ![]() ЃЌ
ЃЌ
МДЕуFЕНBCЕФОрРыЮЊ3Љ![]() ЃЎ
ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
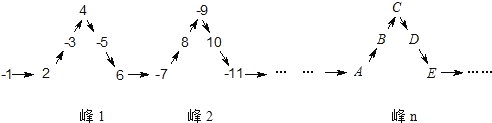
ЁОЬтФПЁПНЋвЛСагаРэЪ§-1ЃЌ2ЃЌ-3ЃЌ4ЃЌ-5ЃЌ6,ЁШчЭМЫљЪОХХСаЃЌИљОнЭМжаЕФХХСаЙцТЩПЩжЊЃЌЁАЗх1ЁБжаЗтЖЅЕФЮЛжУЃЈ![]() ЕФЮЛжУЃЉЪЧгаРэЪ§4ЃЌЁАЗх2ЁБжаЗтЖЅЕФЮЛжУЃЈ
ЕФЮЛжУЃЉЪЧгаРэЪ§4ЃЌЁАЗх2ЁБжаЗтЖЅЕФЮЛжУЃЈ![]() ЕФЮЛжУЃЉЪЧгаРэЪ§-9ЃЌАДДЫЙцТЩХХСаЃЌ2020гІХХдк
ЕФЮЛжУЃЉЪЧгаРэЪ§-9ЃЌАДДЫЙцТЩХХСаЃЌ2020гІХХдк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ,
,![]() ЃЌ
ЃЌ![]() жа________ЕФЮЛжУ.
жа________ЕФЮЛжУ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЁЂ
ЁЂ![]() БпЩЯЕФЕуЃЌЧв
БпЩЯЕФЕуЃЌЧв![]() .
.
ЃЈ1ЃЉЧѓжЄ:![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() дк
дк![]() ФкЃЌ
ФкЃЌ![]() дк
дк![]() ФкЃЌ
ФкЃЌ![]() .
.
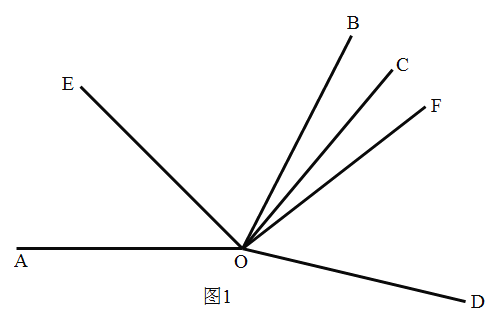
ЃЈ1ЃЉ![]() ДгЭМ1жаЕФЮЛжУШЦЕу
ДгЭМ1жаЕФЮЛжУШЦЕу![]() ФцЪБеыа§зЊЕН
ФцЪБеыа§зЊЕН![]() гы
гы![]() жиКЯЪБЃЌШчЭМ2ЃЌ
жиКЯЪБЃЌШчЭМ2ЃЌ![]()
![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЭМ1жаЕФ![]() ЦНЗж
ЦНЗж![]() ЃЌдђ
ЃЌдђ![]() ДгЭМ1жаЕФЮЛжУШЦЕу
ДгЭМ1жаЕФЮЛжУШЦЕу![]() ФцЪБеыа§зЊЕН
ФцЪБеыа§зЊЕН![]() гы
гы![]() жиКЯЪБЃЌа§зЊСЫЖрЩйЖШЃП
жиКЯЪБЃЌа§зЊСЫЖрЩйЖШЃП
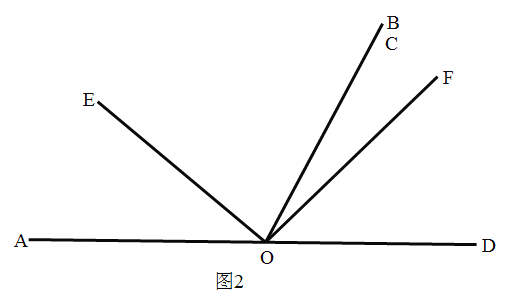
ЃЈ3ЃЉ![]() ДгЭМ2жаЕФЮЛжУШЦЕу
ДгЭМ2жаЕФЮЛжУШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЃЌЪдЮЪЃКдка§зЊЙ§ГЬжа
ЃЌЪдЮЪЃКдка§зЊЙ§ГЬжа![]() ЕФЖШЪ§ЪЧЗёИФБфЃПШєВЛИФБфЃЌЧыЧѓГіЫќЕФЖШЪ§ЃЛШєИФБфЃЌЧыЫЕУїРэгЩ.
ЕФЖШЪ§ЪЧЗёИФБфЃПШєВЛИФБфЃЌЧыЧѓГіЫќЕФЖШЪ§ЃЛШєИФБфЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
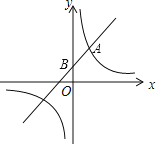
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНkx+bЃЈkЁй0ЃЉОЙ§ЕуBЃЈ0ЃЌ1ЃЉЃЌЧвгыЗДБШР§КЏЪ§yЃН![]() ЃЈmЁй0ЃЉЕФЭМЯѓдкЕквЛЯѓЯогаЙЋЙВЕуAЃЈ1ЃЌ2ЃЉЃЎ
ЃЈmЁй0ЃЉЕФЭМЯѓдкЕквЛЯѓЯогаЙЋЙВЕуAЃЈ1ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЭМЯѓаДГіЕБxШЁКЮжЕЪБЃЌвЛДЮКЏЪ§ЕФжЕаЁгкЗДБШР§КЏЪ§ЕФжЕЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкГЄЗНаЮжНЦЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌШчЭМЃЈaЃЉЫљЪОЃЌНЋГЄЗНаЮжНЦЌ
ЪБЃЌШчЭМЃЈaЃЉЫљЪОЃЌНЋГЄЗНаЮжНЦЌ![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() Тфдк
Тфдк![]() БпЩЯЃЌМЧзїЕу
БпЩЯЃЌМЧзїЕу![]() ЃЌелКлЮЊ
ЃЌелКлЮЊ![]() ЃЌШчЭМЃЈbЃЉЫљЪО.ДЫЪБЃЌЭМЃЈbЃЉжаЯпЖЮ
ЃЌШчЭМЃЈbЃЉЫљЪО.ДЫЪБЃЌЭМЃЈbЃЉжаЯпЖЮ![]() ГЄЪЧ РхУз.
ГЄЪЧ РхУз.
ЃЈ2ЃЉШє![]() РхУзЃЌЯШНЋГЄЗНаЮжНЦЌ
РхУзЃЌЯШНЋГЄЗНаЮжНЦЌ![]() АДЮЪЬтЃЈ1ЃЉЕФЗНЗЈелЕўЃЌдйНЋ
АДЮЪЬтЃЈ1ЃЉЕФЗНЗЈелЕўЃЌдйНЋ![]() би
би![]() ЯђгвЗелЃЌЪЙЕу
ЯђгвЗелЃЌЪЙЕу![]() ТфдкЩфЯп
ТфдкЩфЯп![]() ЩЯЃЌМЧзїЕу
ЩЯЃЌМЧзїЕу![]() .ШєЗелКѓЕФЭМаЮжаЃЌЯпЖЮ
.ШєЗелКѓЕФЭМаЮжаЃЌЯпЖЮ![]() ЃЌЧыИљОнЬтвтЛГіЭМаЮЃЈВнЭМЃЉЃЌВЂЧѓГі
ЃЌЧыИљОнЬтвтЛГіЭМаЮЃЈВнЭМЃЉЃЌВЂЧѓГі![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁАдЊЕЉЁБЦкМфЃЌЦНМлЩЬГЁЖдИУЩЬГЁЩЬЦЗНјааШчЯТЕФгХЛнДйЯњЛюЖЏЃК
ДђелЧАвЛДЮадЙКЮязмН№Жю | гХЛнДыЪЉ |
аЁгкЕШгк 400 дЊ | ВЛгХЛн |
ГЌЙ§ 400 дЊЃЌЕЋВЛГЌЙ§ 600дЊ | АДЪлМлДђОХел |
ГЌЙ§ 600 дЊ | Цфжа 600 дЊВПЗжАЫелгХЛнЃЌГЌЙ§ 600 дЊЕФВПЗжДђСљелгХЛн |
АДЩЯЪігХЛнЬѕМўЃЌШєаЁЛЊвЛДЮадЙКТђЪлМлЮЊ 80 дЊ/МўЕФЩЬЦЗ n МўЪБЃЌЪЕМЪИЖПю 504 дЊЃЌ дђ n=_____.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпy=kx+6ЗжБ№гыxжсЁЂyжсНЛгкЕуEЃЌFЃЌвбжЊЕуEЕФзјБъЮЊЃЈЉ8ЃЌ0ЃЉЃЌЕуAЕФзјБъЮЊЃЈЉ6ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
ЃЈ2ЃЉШєЕуPЃЈxЃЌyЃЉЪЧИУжБЯпЩЯЕФвЛИіЖЏЕуЃЌЧвдкЕкЖўЯѓЯоФкдЫЖЏЃЌЪдаДГіЁїOPAЕФУцЛ§SЙигкxЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉЬНОПЃКЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЁїOPAЕФУцЛ§ЮЊ![]() ЃЌВЂЫЕУїРэгЩЃЎ
ЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЫвТжДЌКЭвЛЫвПьЭЇбиЯрЭЌЕФТЗЯпДгМзИлГіЗЂЪЛЯђввИлЕФЙ§ГЬжаЃЌТЗГЬ![]() ЫцЪБМф
ЫцЪБМф![]() БфЛЏЕФЭМЯёШчЭМЪОЃЈЗжБ№ЪЧе§БШР§КЏЪ§ЕФЭМЯёКЭвЛДЮКЏЪ§ЕФЭМЯёЃЉ.ИљОнЭМжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
БфЛЏЕФЭМЯёШчЭМЪОЃЈЗжБ№ЪЧе§БШР§КЏЪ§ЕФЭМЯёКЭвЛДЮКЏЪ§ЕФЭМЯёЃЉ.ИљОнЭМжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
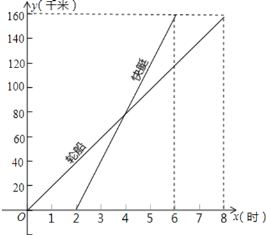
ЃЈ1ЃЉЗжБ№ЧѓГіБэЪОТжДЌКЭПьЭЇааЪЛЙ§ГЬжаТЗГЬ![]() КЭЪБМф
КЭЪБМф![]() жЎМфЕФКЏЪ§НтЮіЪНЃЈВЛвЊЧѓаДГіздБфСПЕФШЁжЕЗЖЮЇЃЉЃЛ
жЎМфЕФКЏЪ§НтЮіЪНЃЈВЛвЊЧѓаДГіздБфСПЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉТжДЌКЭПьЭЇдкЭОжаЃЈВЛАќРЈЦ№ЕуКЭжеЕуЃЉааЪЛЕФЫйЖШЗжБ№ЪЧЖрЩйЃП
ЃЈ3ЃЉПьЭЇГіЗЂЖрГЄЪБМфИЯЩЯТжДЌЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com