
【题目】一艘轮船和一艘快艇沿相同的路线从甲港出发驶向乙港的过程中,路程![]() 随时间
随时间![]() 变化的图像如图示(分别是正比例函数的图像和一次函数的图像).根据图中提供的信息解答下列问题:
变化的图像如图示(分别是正比例函数的图像和一次函数的图像).根据图中提供的信息解答下列问题:
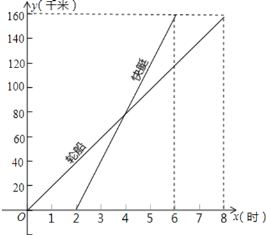
(1)分别求出表示轮船和快艇行驶过程中路程![]() 和时间
和时间![]() 之间的函数解析式(不要求写出自变量的取值范围);
之间的函数解析式(不要求写出自变量的取值范围);
(2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少?
(3)快艇出发多长时间赶上轮船?
【答案】(1)轮船行驶过程的函数式为y=20x.;快艇行驶过程的函数解析式为y=40x80;(2)轮船在途中的行驶速度为20(千米/时);快艇在途中行驶的速度为40(千米/时);(3)快艇出发2小时后赶上轮船.
【解析】
(1)可根据图中给出的信息,用待定系数法分别求出轮船与快艇的函数关系式.
(2)可根据轮船与快艇到乙港时用的时间和走的路程,根据速度=路程÷时间,求出速度是多少.
(3)当快艇追上轮船时两者走的路程相同,根据(1)求出的函数式,让两者的路程相等,即可得出时间的值.
(1)设表示轮船行驶过程的函数式为y=kx.由图象知:
当x=8时,y=160.
∴8k=160,解得:k=20
∴表示轮船行驶过程的函数式为y=20x.
设表示快艇行驶过程的函数解析式为y=ax+b.
由图象知:当x=2时,y=0;当x=6时,y=160
∴![]() ,
,
解得![]()
因此表示快艇行驶过程的函数解析式为y=40x80;
(2)由图象可知,轮船在8小时内行驶了160千米。快艇在4小时内行驶了160千米。
故轮船在途中的行驶速度为160÷8=20(千米/时)
快艇在途中行驶的速度为160÷4=40(千米/时);
(3)设轮船出发x小时后快艇追上轮船。
20x=40x80,
x=4,
则x2=2.
答:快艇出发2小时后赶上轮船.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
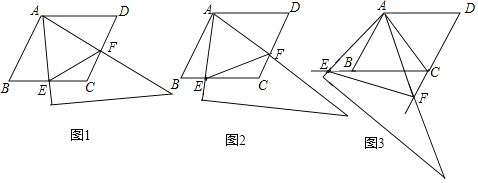
【题目】已知:四边形ABCD是菱形,AB=4,∠ABC=60°,有一足够大的含60°角的直角三角尺的60°角的顶点与菱形ABCD的顶点A重合,两边分别射线CB、DC相交于点E、F,且∠EAP=60°.
(1)如图1,当点E是线段CB的中点时,请直接判断△AEF的形状是 .
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
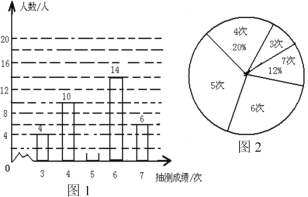
【题目】为了了解某校七年级男生的体能情况,体育老师随即抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2尚不完整的统计图。
(1)本次抽测的男生有 人;
(2)请你将图1的统计图补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,则该校350名九年级男生中,估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1,L2分别表示两辆汽车的s与t的关系.
(1)L1表示哪辆汽车到甲地的距离与行驶时间的关系?
(2)汽车B的速度是多少?
(3)求L1,L2分别表示的两辆汽车的s与t的关系式.
(4)2小时后,两车相距多少千米?
(5)行驶多长时间后,A、B两车相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A'B'C'.若∠A=40°,∠B'=110°,∠BCA'的度数是( )
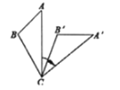
A.110°B.80°C.40°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在“堆石子”游戏中发现:像图(1)中的![]() 这些数据能够表示成正方形,可将其称为正方形数;类似地,像图(2)中的
这些数据能够表示成正方形,可将其称为正方形数;类似地,像图(2)中的![]() 这些数据能够表示成三角形,可将其称为三角形数.
这些数据能够表示成三角形,可将其称为三角形数.

(1)第![]() 个正方形数是 ;第
个正方形数是 ;第![]() 个正方形数是 ;
个正方形数是 ;
(2)第![]() 个三角形数是 ;第
个三角形数是 ;第![]() 个三角形数是 ;
个三角形数是 ;
(3)若将一堆小石子按一定规律摆成下列图形,请求出第![]() 个图形中“●”的个数.
个图形中“●”的个数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
如图,抛物线y=![]() x2﹣
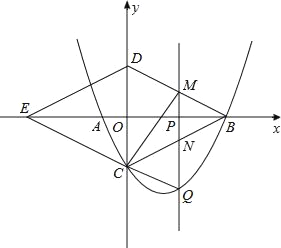
x2﹣![]() x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A,B,C的坐标.
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,M、N分别是边AB、AC的中点,D是边BC延长线上的一点,且![]() ,联结CM、DN.
,联结CM、DN.
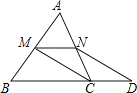
(1)求证:四边形MCDN是平行四边形;
(2)若三角形AMN的面积等于5,求梯形MBDN的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com