
【题目】综合与探究:
如图,抛物线y=![]() x2﹣
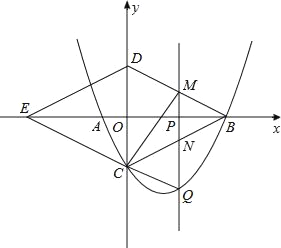
x2﹣![]() x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A,B,C的坐标.
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)点A的坐标为(﹣2,0),点B的坐标为(8,0).点C的坐标为(0,﹣4);
(2)当m=4时,四边形CQMD是平行四边形;
(3)符合题意的点Q的坐标为(﹣2,0)或(6,﹣4).
【解析】试题分析:(1)根据坐标轴上点的特点,可求点A,B,C的坐标.
(2)由菱形的对称性可知,点D的坐标,根据待定系数法可求直线BD的解析式,根据平行四边形的性可得关于m的方程,求得m的值;再根据平行四边形的判定可得四边形CQBM的形状;
(3)分DQ⊥BD,BQ⊥BD两种情况讨论可求点Q的坐标.
试题解析:(1)当y=0时, ![]() x2-
x2-![]() x-4=0,解得x1=-2,x2=8,
x-4=0,解得x1=-2,x2=8,
∵点B在点A的右侧,
∴点A的坐标为(-2,0),点B的坐标为(8,0).
当x=0时,y=-4,
∴点C的坐标为(0,-4).
(2)由菱形的对称性可知,点D的坐标为(0,4).
设直线BD的解析式为y=kx+b,则![]() ,
,
解得k=-![]() ,b=4.
,b=4.
∴直线BD的解析式为y=-![]() x+4.
x+4.
∵l⊥x轴,
∴点M的坐标为(m,-![]() m+4),点Q的坐标为(m,
m+4),点Q的坐标为(m, ![]() m2-
m2-![]() m-4).
m-4).
如图,当MQ=DC时,四边形CQMD是平行四边形,
∴(-![]() m+4)-(
m+4)-(![]() m2-
m2-![]() m-4)=4-(-4).
m-4)=4-(-4).
化简得:m2-4m=0,
解得m1=0(不合题意舍去),m2=4.
∴当m=4时,四边形CQMD是平行四边形.
此时,四边形CQBM是平行四边形.
∵m=4,
∴点P是OB的中点.
∵l⊥x轴,
∴l∥y轴,
∴△BPM∽△BOD,
∴![]() ,
,
∴BM=DM,
∵四边形CQMD是平行四边形,
∴DM∥CQ,DM=CQ
∴BM∥CQ,BM=CQ,
∴四边形CQBM是平行四边形.
(3)抛物线上存在两个这样的点Q,分别是Q1(-2,0),Q2(6,-4).
若△BDQ为直角三角形,可能有三种情形,如图2所示:
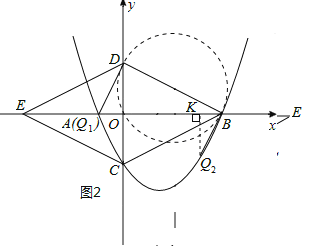
以点Q为直角顶点.
此时以BD为直径作圆,圆与抛物线的交点,即为所求之Q点.
∵P在线段EB上运动,
∴-8≤xQ≤8,而由图形可见,在此范围内,圆与抛物线并无交点,
故此种情形不存在.
以点D为直角顶点.
连接AD,∵OA=2,OD=4,OB=8,AB=10,
由勾股定理得:AD=2![]() ,BD=4
,BD=4![]() ,
,
∵AD2+BD2=AB2,
∴△ABD为直角三角形,即点A为所求的点Q.
∴Q1(-2,0);
以点B为直角顶点.
如图,设Q2点坐标为(x,y),过点Q2作Q2K⊥x轴于点K,则Q2K=-y,OK=x,BK=8-x.
易证△Q2KB∽△BOD,
∴![]() ,即
,即![]() ,整理得:y=2x-16.
,整理得:y=2x-16.
∵点Q在抛物线上,
∴y=![]() x2-
x2-![]() x-4.
x-4.
∴![]() x2-
x2-![]() x-4=2x-16,解得x=6或x=8,
x-4=2x-16,解得x=6或x=8,
当x=8时,点Q2与点B重合,故舍去;
当x=6时,y=-4,
∴Q2(6,-4).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
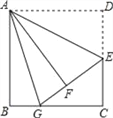
【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市从2018年1月1日开始,禁止燃油助力车上路,于是电动自行车的市场需求量日渐增多.某商店计划最多投入8万元购进A、B两种型号的电动自行车共30辆,其中每辆B型电动自行车比每辆A型电动自行车多500元.用5万元购进的A型电动自行车与用6万元购进的B型电动自行车数量一样.
(1)求A、B两种型号电动自行车的进货单价;
(2)若A型电动自行车每辆售价为2800元,B型电动自行车每辆售价为3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.写出y与m之间的函数关系式;
(3)在(2)的条件下,该商店如何进货才能获得最大利润?此时最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,![]() ,c是-4的相反数,且a,b,c分别是点A.B.C在数轴上对应的数.
,c是-4的相反数,且a,b,c分别是点A.B.C在数轴上对应的数.

(1)求a,b,c的值,并在数轴上标出点A,B,C;
(2)在数轴上,若D到A的距离刚好是3,则D点叫做A的“幸福点”.则A的幸福点D所表示的数应该是_______________.
(3)若动点P从点B出发沿数轴向正方向运动,动点Q同时从点A出发也沿数轴向正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点P可以追上点Q?
(4)在数轴上,若M到A,C的距离之和为6,则M叫做A,C的“幸福中心”.请直接写出所有点M在数轴上对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若变量z是变量y的函数,同时变量y是变量x的函数,那么我们把变量z叫做变量x的“迭代函数”.
例如:z2y3,yx1,则z2x132x1,那么z2x1就是z与x之间的“迭代函数”解析式.
(1)当2006x2020时,zy2,![]() ,请求出z与x之间的“迭代函数”的解析式及z的最小值;
,请求出z与x之间的“迭代函数”的解析式及z的最小值;
(2)若z2ya,yax24axba0,当1x3时,“迭代函数”z的取值范围为1z17,求a和b的值;
(3)已知一次函数yax1经过点1,2,zay2b2ycb4(其中a、b、c均为常数),聪明的你们一定知道“迭代函数”z是x的二次函数,若x1、x2(x1x2)是“迭代函数”z3的两个根,点x3,2是“迭代函数”z的顶点,而且x1、x2、x3还是一个直角三角形的三条边长,请破解“迭代函数”z关于x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从![]() 地出发,晚上到达
地出发,晚上到达![]() 地,约定向东为正方向,当天的航行路程记录如下(单位:千米):
地,约定向东为正方向,当天的航行路程记录如下(单位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)请你帮忙确定![]() 地位于
地位于![]() 地的什么方向,距离
地的什么方向,距离![]() 地多少千米?
地多少千米?
(2)若冲锋舟每千米耗油![]() 升,邮箱容量为
升,邮箱容量为![]() 升,求冲锋舟当天救灾过程中至少还需补充多少升油?
升,求冲锋舟当天救灾过程中至少还需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解重庆市的空气质量情况,我校初2017级“综合实践环境调查”小组从环境监测网随机抽取了若干天的空气质量作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出):


(1)课题小组随机抽取的天数为_______天,请将条形统计图补充完整;
(2)为找出优化环境的措施,“环境治理研讨小组”的同学欲从天气质量为“中度污染”和“重度污染”的样本中随机抽取两天分析污染原因,请用列表或画树状图的方法求出所抽取的两天恰好都是“重度污染”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com