
����Ŀ����֪a�����ĸ�������![]() ��c��-4���෴������a��b��c�ֱ��ǵ�A.B.C�������϶�Ӧ����.
��c��-4���෴������a��b��c�ֱ��ǵ�A.B.C�������϶�Ӧ����.

��1����a��b��c��ֵ�����������ϱ����A��B��C;
��2���������ϣ���D��A�ľ���պ���3����D�����A�����Ҹ�����.��A���Ҹ���D����ʾ����Ӧ����_______________.
��3��������P�ӵ�B�������������������˶�������Qͬʱ�ӵ�A����Ҳ���������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��1����λ���ȣ����˶������P�����ϵ�Q?
��4���������ϣ���M��A��C�ľ���֮��Ϊ6����M����A��C�����Ҹ�������.��ֱ��д�����е�M�������϶�Ӧ����.
���𰸡���1��![]() ��ͼ��������
��ͼ��������
��2��-4��2��
��3���˶�2���P�����ϵ�Q��
��4����M��Ӧ������-1.5��4.5.
��������
��1������������������ظ����ֱ�ӵó������������ϱ�ʾ�������ɣ�
��2�����������ϵĵ��ʾ���ķ����ɵó���D��ʾ���������ֿ��ܣ������д�����ɣ�
��3�����˶�t���P�����ϵ�Q�����������г�������⼴�ɣ�
��4���ֵ�M�ڵ�A��ߣ�AC֮��͵�C�ұ�������������г����̿ɵý�.
�⣺��1��������ã�![]() ��
��
�����ϱ�ʾ����ͼ��

��2����D��A���ʱ��D��ʾ����Ϊ-4��
��D��A�ұ�ʱ��D��ʾ����Ϊ2��
�ʴ�Ϊ-4��2��
��3�����˶�t���P�����ϵ�Q��
���P��ʾ��-5+3t����Q��ʾt-1��
������ã�-5+3t=t-1��
��ã�t=2��
���˶�2���P�����ϵ�Q��
��4�����M��ʾ������m,�ֵ�M�ڵ�A��ߣ�A��C֮��͵�C�ұ������������.
��M�ڵ�A���ʱ��AM=-1-m,CM=4-m,
-1-m+4-m=6,���m=-1.5;
��M�ڵ�A��C֮��ʱ��AM+CM=AC=5,�ʴ�ʱm�⣻
��M�ڵ�C�ұ�ʱ��AM=m+1,CM=m-4,
m+1+ m-4=6. ���m=4.5;
��ʹ��M��A��C�ľ���֮�͵���6����M��Ӧ������-1.5��4.5.


 �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��ڽ����ڼ俪չ�Żݴ������������ԭ�۳���200Ԫ����Ʒ������200Ԫ�IJ��ֿ������ܴ����Ż���������Ʒ��ʵ�ʸ�����y����λ��Ԫ������Ʒԭ��x����λ��Ԫ��֮��ĺ�����ϵ��aͼ����ͼ��ʾ����ͼ��a��ֵ�ǣ�������
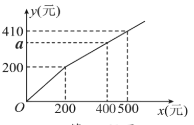
A.300B.320C.340D.360
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڵȱ�������ABC�У���B����C ��ƽ���߽��ڵ�O��OB��OC�Ĵ�ֱƽ���߽�BC��E��F����֤��BE=EF=FC
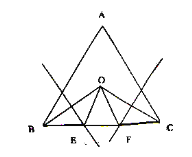
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
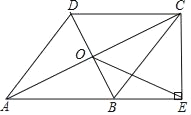
����Ŀ����ͼ�����ı���ABCD�У�AB��DC��AB��AD���Խ���AC��BD���ڵ�O��ACƽ����BAD������C��CE��AB��AB���ӳ����ڵ�E������OE��
��1����֤���ı���ABCD�����Σ�
��2����AB��![]() ��BD��2����OE�ij���
��BD��2����OE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽����
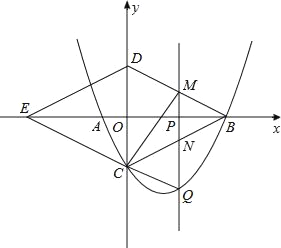
��ͼ��������y=![]() x2��
x2��![]() x��4��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
x��4��x�ύ��A��B���㣨��B�ڵ�A���Ҳࣩ����y�ύ�ڵ�C������BC����BCΪһ�ߣ���OΪ�Գ�����������BDEC����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
��1�����A��B��C�����꣮
��2������P���߶�OB���˶�ʱ��ֱ��l�ֱ�BD��BC�ڵ�M��N����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ���ʱ�����ж��ı���CQBM����״����˵�����ɣ�
��3������P���߶�EB���˶�ʱ���Ƿ���ڵ�Q��ʹ��BDQΪֱ�������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪABC�����Բ��DΪOC��AB�Ľ��㣬EΪ�߶�OC�ӳ�����һ�㣬��EACABC.
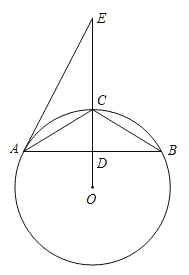
��1����֤��ֱ��AE�ǡ�O�����ߣ�
��2����DΪAB���е㣬CD3��AB8.
�����O�İ뾶������ABC������I����O�ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() �ϵ��е㣬
�ϵ��е㣬![]() ������ֱ��ǵ�
������ֱ��ǵ�![]() .
.
(1)��![]() ����֤��
����֤��![]() ��
��
(2)��![]() ����֤���ı���
����֤���ı���![]() �Ǿ���.
�Ǿ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ĵ�λ����Ϊ1��
![]()
��1�������A��D��ʾ������Ϊ�෴������ô��B��ʾ�����Ƕ��٣�
��2�������B��D��ʾ������Ϊ�෴������ôͼ�б�ʾ���ĸ����У���һ���ʾ�����ľ���ֵ���Ϊʲô��
��3������BΪԭ��ʱ��������һ��M��A�ľ����ǵ�M��D�ľ����2�������M����ʾ������____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=3��AC=4��BC=5��PΪ��BC��һ���㣬PE��AB��E��PF��AC��F��MΪEF�е㣬��AM����СֵΪ_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com