
【题目】如图,⊙O为ABC的外接圆,D为OC与AB的交点,E为线段OC延长线上一点,且EACABC.
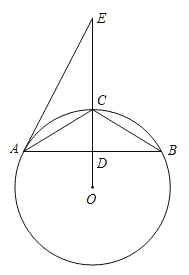
(1)求证:直线AE是⊙O的切线;
(2)若D为AB的中点,CD3,AB8.
①求⊙O的半径;②求ABC的内心I到点O的距离.
【答案】(1)见解析;(2)①⊙O的半径![]() ;②ABC的内心I到点O的距离为
;②ABC的内心I到点O的距离为![]() .
.
【解析】
(1)连接AO,证得EACABC=![]() ,
,![]() ,则EAO=EAC+CAO=
,则EAO=EAC+CAO=![]() ,从而得证;
,从而得证;
(2)①设⊙O的半径为r,则OD=r-3,在△AOD中,根据勾股定理即可得出②作出ABC的内心I,过I作AC,BC的垂线,垂足分别为F,G.设内心I到各边的距离为a,由面积法列出方程求解可得答案。
(1)如图,连接AO
则EACABC=![]() .
.
又∵AO=BO,
∴ACO=CAO=![]()
∴EAO=EAC+CAO=![]() AOC +
AOC +![]() =
=![]()
∴EA⊥AO
∴直线AE是⊙O的切线;
(2)①设⊙O的半径为r,则OD=r-3,
∵D为AB的中点,
∴OC⊥AB,ADO=![]() ,AD=4
,AD=4
∴![]() ,即
,即![]()
解得![]()
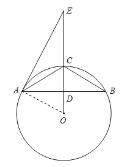
②如下图,
∵D为AB的中点,
∴![]()
且CO是![]() 的平分线,则内心I在CO上,连接AI,BI,过I作AC,BC的垂线,垂足分别为F,G.
的平分线,则内心I在CO上,连接AI,BI,过I作AC,BC的垂线,垂足分别为F,G.

易知DI=FI=GI,设其长为a.由面积可知:
![]()
即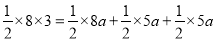
解得![]()
∴![]()
∴ABC的内心I到点O的距离为![]()


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】某原料仓库一天的原料进出记录如下表(运进用正数表示,运出用负数表示);
每次进出数量(单位:吨) | -3 | 4 | -1 | 2 | -5 |
进出次数 | 2 | 1 | 3 | 3 | 2 |
(1)这天仓库的原料比原来增加或减少了多少吨?
(2)根据实际情况,现有两种方案:
方案一:运进每吨原料费用5元,运出每吨原料费用8元;
方案二:不管运进还是运出费用都是每吨原料6元;
从节约运费的角度考虑,选用哪一种方案较合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小华用除了正面的数字不同其他完全相同的4张卡片玩游戏,卡片上的数字分别是2、4、5、6,他俩将卡片洗匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的卡片不放回
(1)若小明恰好抽到了标注4的卡片,直接写出小华抽出的卡片上的数字比4大的概率是多少;
(2)小明、小华约定,若小明抽到的卡片的标注数字比小华的大,则小明胜:反之,则小明负,你认为这个游戏是否公平?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织七年级学生体育健康抽测,(1)班25名学生的成绩(满分为100分)统计如下:
90,74,88,65,98,76,81,42,85,70,55,80,95,88,72,87,61,56,76,66,78,72,82,63,100.
(1)90分及以上为A级,75-89分为B级,60-74分为C级,60分以下为D级,请把下面表格补充完整,并将图中的条形图补充完整;
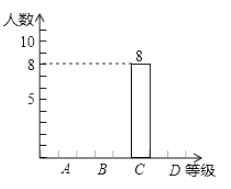
等级 | A | B | C | D |
人数 | 8 |
(2)该校七年级共有1000名学生,如果60分以上为合格,请估计七年级有多少人合格?
(3)请选择合适的统计图表示出抽测中每一个等级的人数占总人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,![]() ,c是-4的相反数,且a,b,c分别是点A.B.C在数轴上对应的数.
,c是-4的相反数,且a,b,c分别是点A.B.C在数轴上对应的数.

(1)求a,b,c的值,并在数轴上标出点A,B,C;
(2)在数轴上,若D到A的距离刚好是3,则D点叫做A的“幸福点”.则A的幸福点D所表示的数应该是_______________.
(3)若动点P从点B出发沿数轴向正方向运动,动点Q同时从点A出发也沿数轴向正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点P可以追上点Q?
(4)在数轴上,若M到A,C的距离之和为6,则M叫做A,C的“幸福中心”.请直接写出所有点M在数轴上对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实验室:
点A.B在数轴上分别表示有理数a.b,A.B两点之间的距离表示为AB,在数轴上A.B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示2和5的两点之间的距离是_________,数轴上表示1和-3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是-2,则点A和B之间的距离是 ,若AB=2,那么x为 ;
(3)当x是 时,代数式![]() ;
;
(4)若点A表示的数-1,点B与点A的距离是10,且点B在点A的右侧,动点P.Q同时从A.B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度。当PQ=1时,求运动时间?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,ABCO的顶点A,B的坐标分别是A(3,0),B(0,2),动点P在直线y=![]() x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与四边形ABCO的边所在直线相切时,P点的坐标为_____.
x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与四边形ABCO的边所在直线相切时,P点的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,我们把任意形如:![]() 的五位自然数(其中
的五位自然数(其中![]() ,
,![]() ,
,![]() )称之为喜马拉雅数,例如:在自然数
)称之为喜马拉雅数,例如:在自然数![]() 中,
中,![]() ,所以
,所以![]() 就是一个喜马拉雅数.并规定:能被自然数
就是一个喜马拉雅数.并规定:能被自然数![]() 整除的最大的喜马拉雅数记为
整除的最大的喜马拉雅数记为![]() ,能被自然数
,能被自然数![]() 整除的最小的喜马拉雅数记为
整除的最小的喜马拉雅数记为![]() .
.
(1)求证:任意一个喜马拉雅数都能被3整除;
(2)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com