
【题目】已知,我们把任意形如:![]() 的五位自然数(其中
的五位自然数(其中![]() ,
,![]() ,
,![]() )称之为喜马拉雅数,例如:在自然数
)称之为喜马拉雅数,例如:在自然数![]() 中,
中,![]() ,所以
,所以![]() 就是一个喜马拉雅数.并规定:能被自然数
就是一个喜马拉雅数.并规定:能被自然数![]() 整除的最大的喜马拉雅数记为
整除的最大的喜马拉雅数记为![]() ,能被自然数
,能被自然数![]() 整除的最小的喜马拉雅数记为
整除的最小的喜马拉雅数记为![]() .
.
(1)求证:任意一个喜马拉雅数都能被3整除;
(2)求![]() 的值.
的值.
【答案】(1)答案见解析;(2)112221.
【解析】分析:(1)根据喜马拉雅数的定义求出各个数位上的数字之和;(2)根据能被自然数8整除的最小的喜马拉雅数记为![]() 的整除的特征,与各数位上的数字的特点求得I(8).
的整除的特征,与各数位上的数字的特点求得I(8).
详解:(1)各数位数字之和为:
a+b+c+b+a=2a+2b+c=2a+2b+(a+b)=3(a+b).
∵a,b是整数,
∴a+b是整数.
∴任意一个喜马拉雅数都能被3整除
(2)根据题意得:F(3)=90909.
I(8)=![]() =1263a+139b-
=1263a+139b-![]() ,
,
∵喜马拉雅数能被8整除,
∴3a+2b能被8整除.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴3a+2b=8或16或24.
则I(8)=21312.
∴F(3)+I(8)=90909+21312=112221.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O为ABC的外接圆,D为OC与AB的交点,E为线段OC延长线上一点,且EACABC.
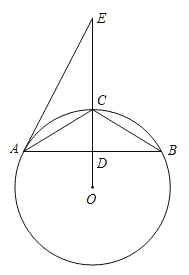
(1)求证:直线AE是⊙O的切线;
(2)若D为AB的中点,CD3,AB8.
①求⊙O的半径;②求ABC的内心I到点O的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
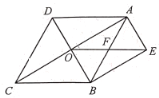
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判断△ABC是直角三角形的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年水果大丰收,A,B两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A基地运往甲、乙两销售点的费用分别为每件40元和20元,从B基地运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件.
(1)设从A基地运往甲销售点水果x件,总运费为W元,请用含x的代数式表示W,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是边长为![]() 的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是
的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是![]() .其中正确结论是( )
.其中正确结论是( )

A. ①③ B. ②③ C. ②③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某花园护栏是用直径为80厘米的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度就增加a厘米(a>0).设半圆形条钢的总个数为x(x为正整数),护栏总长度为y厘米.
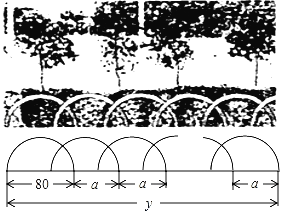
(1)当a=50,x=2时,护栏总长度y为 厘米;
(2)当a=60时,用含x的代数式表示护栏总长度y(结果要化简);
(3)在(2)的条件下,若要使护栏总长度为50x+430,请求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李的住房结构如图所示。(单位:米)
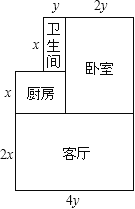
(1)小李打算把卧室和客厅铺上木地板,请你帮他算一算,他至少需要买多少平方米的木地板?
(2)当x=6,y=3时,小李住房的总面积是多少平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com