练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

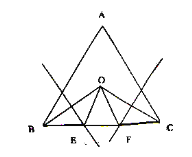
    【题目】如图所示，在等边三角形ABC中，∠B、∠C 的平分线交于点O，OB和OC的垂直平分线交BC于E、F，求证：BE=EF=FC

    【答案】见解析

    【解析】

    先根据线段的垂直平分线的性质和角平分线性质得到有关的角和线段之间的等量关系：∠OBC=∠OCB=30°，OE=BE，OF=FC；再利用三角形的外角等于不相邻的两内角和求出∠OEF=60°，∠OFE=60°．从而判定△OEF是等边三角形即OE=OF=EF，通过线段的等量代换求证即可．

    解：在等边三角形ABC中．


    ∵∠ABC、∠ACB的平分线交于点O，OB和OC的垂直平分线交BC于E、F，
    ∴∠OBC=∠OCB=30°，OE=BE，OF=FC．
    ∴∠OEF=60°，∠OFE=60°．
    ∴OE=OF=EF．
    ∴BE=EF=FC．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】每年5月的第二个星期日即为母亲节，“父母恩深重，恩怜无歇时”，许多市民喜欢在母亲节为母亲送鲜花，感恩母亲，祝福母亲. 节日前夕，某花店采购了一批鲜花礼盒，成本价为30元每件，分析上一年母亲节的鲜花礼盒销售情况，得到了如下数据，同时发现每天的销售量（件）是销售单价（元/件）的一次函数.

    销售单价 (元/件)

    …

    30

    40

    50

    60

    …

    每天销售量 (件)

    …

    350

    300

    250

    200

    …

    （1）求出与的函数关系；

    （2）物价局要求,销售该鲜花礼盒获得的利润不得高于100﹪：

    ①当销售单价取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价)；

    ②试确定销售单价取何值时，花店销该鲜花礼盒每天获得的利润（元）最大？并求出花店销该鲜花礼盒每天获得的最大利润.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，M为AD的中点，BM＝CM．

    求证：（1）△ABM≌△DCM；

    （2）四边形ABCD是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是常见的安全标记，其中是轴对称图形的是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线，我们把这条封闭曲线成为“蛋线”．已知点C的坐标为（0，﹣ ），点M是抛物线C2：y=mx2﹣2mx﹣3m（m＜0）的顶点．

    （1）求A、B两点的坐标；

    （2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；

    （3）当△BDM为直角三角形时，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明、小华用除了正面的数字不同其他完全相同的4张卡片玩游戏，卡片上的数字分别是2、4、5、6，他俩将卡片洗匀后，背面朝上放置在桌面上，小明先抽，小华后抽，抽出的卡片不放回

    （1）若小明恰好抽到了标注4的卡片，直接写出小华抽出的卡片上的数字比4大的概率是多少；

    （2）小明、小华约定，若小明抽到的卡片的标注数字比小华的大，则小明胜：反之，则小明负，你认为这个游戏是否公平？请用树状图或列表法说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为12的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G.则BG的长为（　　）

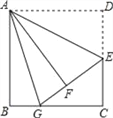
    A. 5 B. 4 C. 3 D. 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a是最大的负整数，，c是-4的相反数，且a，b，c分别是点A.B.C在数轴上对应的数.

    （1）求a，b，c的值，并在数轴上标出点A，B，C;

    （2）在数轴上，若D到A的距离刚好是3，则D点叫做A的“幸福点”.则A的幸福点D所表示的数应该是_______________.

    （3）若动点P从点B出发沿数轴向正方向运动，动点Q同时从点A出发也沿数轴向正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒1个单位长度，求运动几秒后，点P可以追上点Q?

    （4）在数轴上，若M到A，C的距离之和为6，则M叫做A，C的“幸福中心”.请直接写出所有点M在数轴上对应的数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系O中，正方形A1B1C1O、A2B2C2B1、A3B3C3B2，…， 按图所示的方式放置．点A1、A2、A3，…和点B1、B2、B3，…分别在直线和轴上．已知C1（1，-1），C2（， ），则点A3的坐标是________________________．

    查看答案和解析>>

    同步练习册答案