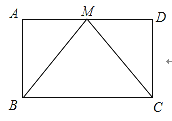
【题目】如图，在ABCD中，M为AD的中点，BM＝CM．
求证：（1）△ABM≌△DCM；
（2）四边形ABCD是矩形．
【答案】（1）详见解析；（2）详见解析；
【解析】
（1）由四边形ABCD是平行四边形，得出AB=CD，又由M为AD的中点，得出AM=MD，又AB=CD，AM=MD，BM=CM，故△ABM ≌△DCM（SSS）；
（2）根据（1）中△ABM≌△DCM，得出∠BAD=∠CDA，又四边形ABCD是平行四边形，∠BAD+∠CDA=180°，得出∠BAD=∠CDA=90°，故可判定四边形ABCD是矩形.
证明：（1）∵四边形ABCD是平行四边形
∴AB=CD
∵M为AD的中点
∴AM=MD
∵AB=CD，AM=MD，BM=CM
∴△ABM ≌△DCM（SSS）
（2）∵△ABM≌△DCM
∴∠BAD=∠CDA
又∵四边形ABCD是平行四边形
∵∠BAD+∠CDA=180°
∴∠BAD=∠CDA=90°
∴四边形ABCD是矩形.
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案科目：初中数学 来源： 题型：
【题目】周末，小明和爸爸在400米的环形跑道上骑车锻炼，他们在同一地点沿着同一方向同时出发，骑行结束后两人有如下对话：
（1）他们的对话内容，求小明和爸爸的骑行速度，
（2）一次追上小明后，在第二次相遇前，再经过多少分钟，小明和爸爸相距50m？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市为了鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过20立方米时，按2元／立方米计费；月用水量超过20立方米时，其中的20立方米仍按2元／立方米收费，超过部分按2.6元／立方米计费．设每户家庭用水量为x立方米时，应交水费y元．
（1）当
时，y= （用含x的代数式表示）；
当
时，y= （用含x的代数式表示）；
（2）小明家第二季度交纳水费的情况如下：
月份 | 四月份 | 五月份 | 六月份 |
交费金额 | 30元 | 34元 | 47.8元 |
小明家这个季度共用水多少立方米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店在节日期间开展优惠促销活动：凡购买原价超过200元的商品，超过200元的部分可以享受打折优惠若购买商品的实际付款金额y（单位：元）与商品原价x（单位：元）之间的函数关系的a图象如图所示，则图中a的值是（ ）
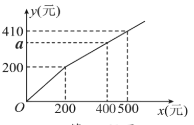
A.300B.320C.340D.360
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小虫从点A出发在一条直线上来回爬行，假定向右爬行的路程记为正数，向左爬行的路程记为负数，爬行的路程依次为：（单位：cm）①+5，②-3，③+10，④-8，⑤-6，⑥+11，⑦-9．
（1）小虫最后是否回到出发点A，说明理由；
（2）小虫在第几次爬行后离点A最远，此时距离点A多少厘米？
（3）在爬行过程中，如果每爬行1厘米奖励一粒芝麻，那么小虫一共得到多少粒芝麻？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，图（1）中含“○”的矩形有1个，图（2）中含“○”的矩形有7个，图（3）中含“○”的矩形有17个，按此规律，图（6）中含“○”的矩形有（ ）
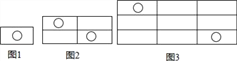
A. 70 B. 71 C. 72 D. 73
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某县教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动．某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：
（1）在这次调查中，喜欢篮球项目的同学有 人，在扇形统计图中，“乒乓球”的百分比为 %，如果学校有800名学生，估计全校学生中有 人喜欢篮球项目．
（2）请将条形统计图补充完整．
（3）在被调查的学生中，喜欢篮球的有2名女同学，其余为男同学．现要从中随机抽取2名同学代表班级参加校篮球队，请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
