
����Ŀ��ij��Ϊ�˹��������Լ��ˮ�����÷ֶμƷѵķ������¼���ÿ����ͥ��ˮ�ѣ�����ˮ��������20������ʱ����2Ԫ�������Ʒѣ�����ˮ������20������ʱ�����е�20��������2Ԫ���������շѣ��������ְ�2.6Ԫ�������Ʒѣ���ÿ����ͥ��ˮ��Ϊx������ʱ��Ӧ��ˮ��yԪ��
��1����![]() ʱ��y= ���ú�x�Ĵ���ʽ��ʾ����
ʱ��y= ���ú�x�Ĵ���ʽ��ʾ����
��![]() ʱ��y= ���ú�x�Ĵ���ʽ��ʾ����
ʱ��y= ���ú�x�Ĵ���ʽ��ʾ����
��2��С���ҵڶ����Ƚ���ˮ�ѵ�������£�
�·� | ���·� | ���·� | ���·� |
���ѽ�� | 30Ԫ | 34Ԫ | 47.8Ԫ |
С����������ȹ���ˮ���������ף�
���𰸡���1��y=2x��y=2.6x-12����2��55������.
��������
��1����Ϊ����ˮ��������20m3ʱ����2Ԫ/m3�Ʒѣ�
���Ե�0��x��20ʱ��y��x�ĺ�������ʽ��y=2x��
��Ϊ����ˮ������20m3ʱ�����е�20m3��2Ԫ/m3�շѣ��������ְ�2.6Ԫ/m3�Ʒѣ�
���Ե�x��20ʱ��y��x�ĺ�������ʽ��y=2��20+2.6��x-20������y=2.6x-12��
��2��������ɵã���Ϊ���·ݡ����·ݽɷѽ�����40Ԫ��������y=2x������ˮ�������·ݽɷѽ���40Ԫ��������y=2.6x-12������ˮ����
��2x=30����ã�x=15�������·���ˮ15 m3��
2x=34����ã�x=17�������·���ˮ17 m3��
2.6x-12=47.8����ã�x=23�������·���ˮ23 m3��
15+17+23=55 m3��
��С����������ȹ���ˮ55������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ӿ��ÿ���ļ��Ƴ�������Ӿ���ѷ�ʽ����ʽһ���ȹ����Ա֤��ÿ�Ż�Ա֤100Ԫ��ֻ�ޱ��˵���ʹ�ã�ƾ֤��Ӿÿ���ٸ���5Ԫ����ʽ�����������Ա֤��ÿ����Ӿ����9Ԫ��
��С���ƻ������ļ���Ӿ����Ϊx��xΪ����������
��I���������⣬��д�±���
��Ӿ���� | 10 | 15 | 20 | �� | x |
��ʽһ���ܷ��ã�Ԫ�� | 150 | 175 | ______ | �� | ______ |
��ʽ�����ܷ��ã�Ԫ�� | 90 | 135 | ______ | �� | ______ |
��������С���ƻ������ļ���Ӿ���ܷ���Ϊ270Ԫ��ѡ�����ָ��ѷ�ʽ������Ӿ�Ĵ����Ƚ϶ࣿ
��������x>20ʱ��С��ѡ�����ָ��ѷ�ʽ�����㣿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�κ���y=-2x+4�����н��۴������(����)
A. ������ͼ����x��Ľ���������![]()
B. ����ֵ���Ա������������С
C. ������ͼ������������
D. ������ͼ������ƽ��4����λ���ȵ�![]() ��ͼ��
��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ��5�µĵڶ��������ռ�Ϊĸ�ڣ�����ĸ�����أ�������Ъʱ������������ϲ����ĸ��Ϊĸ�����ʻ����ж�ĸ�ף�ף��ĸ��. ����ǰϦ��ij����ɹ���һ���ʻ���У��ɱ���Ϊ30Ԫÿ����������һ��ĸ�ڵ��ʻ��������������õ����������ݣ�ͬʱ����ÿ���������![]() �����������۵���
�����������۵���![]() ��Ԫ/������һ�κ���.
��Ԫ/������һ�κ���.
���۵��� | �� | 30 | 40 | 50 | 60 | �� |
ÿ�������� | �� | 350 | 300 | 250 | 200 | �� |
��1�����![]() ��
��![]() �ĺ�����ϵ��
�ĺ�����ϵ��
��2����۾�Ҫ��,���۸��ʻ���л�õ����ø���100����
�������۵���![]() ȡ��ֵʱ,�û��������ʻ����ÿ���õ�����Ϊ5000Ԫ?(����=�����ܼ�-�ɱ���)��
ȡ��ֵʱ,�û��������ʻ����ÿ���õ�����Ϊ5000Ԫ?(����=�����ܼ�-�ɱ���)��
����ȷ�����۵���![]() ȡ��ֵʱ�����������ʻ����ÿ���õ�����
ȡ��ֵʱ�����������ʻ����ÿ���õ�����![]() ��Ԫ�����������������ʻ����ÿ���õ��������.
��Ԫ�����������������ʻ����ÿ���õ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з�ʽ���̽�Ӧ���⣺����ֲ���ڣ�ijУʦ������ѧУ20ǧ�Ĺ�·��ֲ����һ��ʦ�������г����ߣ�����16ǧ����ʦ�����������������ͬʱ�����֪�������ٶȱ����г����ٶ�ÿСʱ��60ǧ�ף������ֳ����ٶȸ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������ACΪֱ������O����AB��D������O��OE��AB����BC��E��
��1����֤��EDΪ��O�����ߣ�
��2�������O�İ뾶Ϊ![]() ��ED=2���ӳ�EO����O��F������DF��AF������ADF�������
��ED=2���ӳ�EO����O��F������DF��AF������ADF�������

���𰸡���1��֤������������2��![]()
�������������������1����������OD����OE��AB������ƽ��������������ε����ʣ���֤��![]() ��
��![]() ���ɵ�
���ɵ�![]() �����֤��
�����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2������CD������ֱ�����Ե�Բ�ܽ���ֱ�ǣ����ɵ�![]() ���ù��ɶ����������
���ù��ɶ����������![]() �ij�������OE��AB��֤��
�ij�������OE��AB��֤��![]() �������������εĶ�Ӧ�߳ɱ������������
�������������εĶ�Ӧ�߳ɱ������������![]() �ij���Ȼ���������Ǻ�����֪ʶ�����
�ij���Ȼ���������Ǻ�����֪ʶ�����![]() ��
��![]() �ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
�ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
���������(1)֤��������OD��

��OE��AB��
���COE=��CAD����EOD=��ODA��
��OA=OD,
���OAD=��ODA��
���COE=��DOE��
�ڡ�COE�͡�DOE�У�
 ���COE�ա�DOE(SAS)��
���COE�ա�DOE(SAS)��
![]()
��ED��OD��
��ED��![]() �����ߣ�
�����ߣ�
(2)����CD����OE��M��
��Rt��ODE��
��OD=32��DE=2��
![]()
��OE��AB��
���COE�ס�CAB��
![]() ��AB=5��
��AB=5��
��AC��ֱ����
![]()
![]()
![]()
![]()
��EF��AB��
![]()
![]()
![]()
��S��ADF=S����ABEFS����DBEF
![]()
���ADF�����Ϊ![]()

�����͡������
��������
25
����Ŀ������Ŀ����֪��������y=ax2+ax+b��a��0����ֱ��y=2x+m��һ��������M��1��0������a��b��
��1����b��a�Ĺ�ϵʽ�������ߵĶ���D���꣨��a�Ĵ���ʽ��ʾ����
��2��ֱ���������ߵ�����һ�������ΪN������DMN�������a�Ĺ�ϵʽ��
��3��a=��1ʱ��ֱ��y=��2x���������ڵڶ������ڵ�G����G��H����ԭ��Գƣ��ֽ��߶�GH��y������ƽ��t����λ��t��0�������߶�GH����������������ͬ�Ĺ����㣬����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
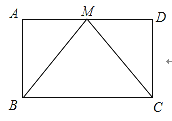
����Ŀ����ͼ����ABCD�У�MΪAD���е㣬BM��CM��
��֤����1����ABM�ա�DCM��
��2���ı���ABCD�Ǿ��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ12��������ABCD�У�E�DZ�CD���е㣬����ADE��AE��������AFE���ӳ�EF��BC�ڵ�G.��BG�ij�Ϊ��������
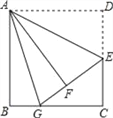
A. 5 B. 4 C. 3 D. 2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com