练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列图形中，既是轴对称图形又是中心对称图形的是（　　）

    A. B. C. D.

    【答案】D

    【解析】

    轴对称图形的定义: 平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形.

    中心对称图形的定义: 在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形.

    根据定义，A、B选项的图形是轴对称图形，C选项的图形是中心对称图形，只有D符合题意.

    A选项图形沿一条直线折叠，直线两旁的部分能够完全重合，是轴对称图形，不符合题意.

    B选项图形沿一条直线折叠，直线两旁的部分能够完全重合的图形，是轴对称图形，不符合题意.

    C选项图形绕着中心点旋转180°，旋转后的图形能与原来的图形重合，是中心对称图形，不符合题意.

    D选项图形既是沿一条直线折叠，直线两旁的部分能够完全重合的图形，又是沿一条直线折叠，直线两旁的部分能够完全重合的图形，绕着中心点旋转180°，旋转后的图形能与原来的图形重合，所以既是轴对称图形又是中心对称图形，符合题意.

    故答案为D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某化妆品公司每月付给销售人员的工资有两种方案．方案一：没有底薪，只拿销售提成；方案二：底薪加销售提成．设x（件）是销售商品的数量，y（元）是销售人员的月工资．如图所示，y1为方案一的函数图象，y2为方案二的函数图象．已知每件商品的销售提成方案二比方案一少8元．从图中信息解答如下问题（注：销售提成是指从销售每件商品得到的销售额中提取一定数量的费用）：

    （1）求y1的函数解析式；

    （2）请问方案二中每月付给销售人员的底薪是多少元？

    （3）小丽应选择哪种销售方案，才能使月工资更多？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小刘对本班同学的业余兴趣爱好进行了一次调查，她根据采集到的数据，绘制了下面的图1和图2．

    请你根据图中提供的信息，解答下列问题：

    （1）在图1中，将“书画”部分的图形补充完整；

    （2）在图2中，求出“球类”部分所对应的圆心角的度数，并分别写出爱好“音乐”、“书画”、“其它”的人数占本班学生数的百分数；

    （3）观察图1和图2，你能得出哪些结论（只要写出一条结论）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为了鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过20立方米时，按2元／立方米计费；月用水量超过20立方米时，其中的20立方米仍按2元／立方米收费，超过部分按2.6元／立方米计费．设每户家庭用水量为x立方米时，应交水费y元．

    （1）当时，y= （用含x的代数式表示）；

    当时，y= （用含x的代数式表示）；

    （2）小明家第二季度交纳水费的情况如下：

    月份

    四月份

    五月份

    六月份

    交费金额

    30元

    34元

    47.8元

    小明家这个季度共用水多少立方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，四边形是正方形，点是边的中点， ，且交正方形的外角平分线于点请你认真阅读下面关于这个图形的探究片段，完成所提出的问题.

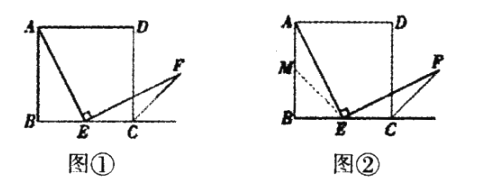
    （1）探究1：小强看到图①后，很快发现这需要证明AE和EF所在的两个三角形全等，但△ABE和△ECF显然不全等（个直角三角形，一个钝角三角形）考虑到点E是边BC的中点，因此可以选取AB的中点M（如图②），连接EM后尝试着去证明就行了.随即小强写出了如下的证明过程：

    证明：如图②，取AB的中点M，连接EM.

    ∵

    ∴

    又∵

    ∴

    ∵点E、M分别为正方形的边BC和AB的中点，

    ∴

    ∴是等腰直角三角形，

    ∴

    又∵是正方形外角的平分线，

    ∴，∴

    ∴

    ∴，

    ∴

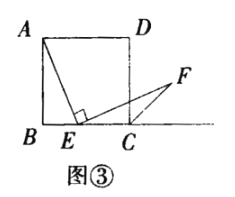
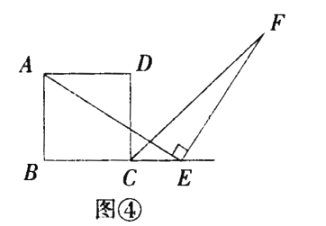
    （2）探究2：小强继续探索，如图③，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”，其余条件不变，发现AE=EF仍然成立小强进一步还想试试，如图④，若把条件“点E是边BC的中点”为“点E是边BC延长线上的一点”，其余条件仍不变，那么结论AE=EF仍然成立请你选择图③或图④中的一种情况写出证明过程给小强看.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店在节日期间开展优惠促销活动：凡购买原价超过200元的商品，超过200元的部分可以享受打折优惠若购买商品的实际付款金额y（单位：元）与商品原价x（单位：元）之间的函数关系的a图象如图所示，则图中a的值是（　　）

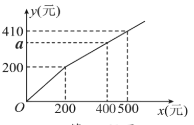
    A.300B.320C.340D.360

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小虫从点A出发在一条直线上来回爬行，假定向右爬行的路程记为正数，向左爬行的路程记为负数，爬行的路程依次为：（单位：cm）①+5，②-3，③+10，④-8，⑤-6，⑥+11，⑦-9．

    （1）小虫最后是否回到出发点A，说明理由；

    （2）小虫在第几次爬行后离点A最远，此时距离点A多少厘米？

    （3）在爬行过程中，如果每爬行1厘米奖励一粒芝麻，那么小虫一共得到多少粒芝麻？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某县教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动．某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：

    （1）在这次调查中，喜欢篮球项目的同学有　 　人，在扇形统计图中，“乒乓球”的百分比为　 　%，如果学校有800名学生，估计全校学生中有　 　人喜欢篮球项目．

    （2）请将条形统计图补充完整．

    （3）在被调查的学生中，喜欢篮球的有2名女同学，其余为男同学．现要从中随机抽取2名同学代表班级参加校篮球队，请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与探究：

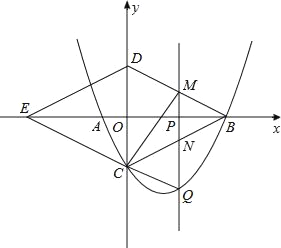
    如图，抛物线y=x2﹣x﹣4与x轴交与A，B两点（点B在点A的右侧），与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．

    （1）求点A，B，C的坐标．

    （2）当点P在线段OB上运动时，直线l分别交BD，BC于点M，N．试探究m为何值时，四边形CQMD是平行四边形，此时，请判断四边形CQBM的形状，并说明理由．

    （3）当点P在线段EB上运动时，是否存在点Q，使△BDQ为直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案