
【题目】如图①,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形的外角平分线
交正方形的外角平分线![]() 于点
于点![]() 请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
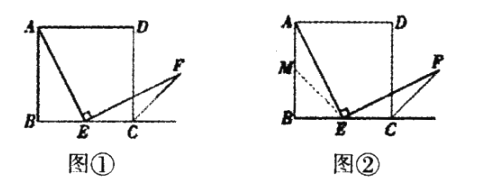
(1)探究1:小强看到图①后,很快发现![]() 这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明
这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明![]() 就行了.随即小强写出了如下的证明过程:
就行了.随即小强写出了如下的证明过程:
证明:如图②,取AB的中点M,连接EM.
∵![]()
∴![]()
又∵![]()
∴![]()
∵点E、M分别为正方形的边BC和AB的中点,
∴![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴![]()
又∵![]() 是正方形外角的平分线,
是正方形外角的平分线,
∴![]() ,∴
,∴![]()
∴![]()
∴![]() ,
,
∴![]()
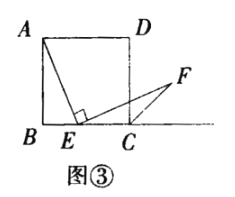
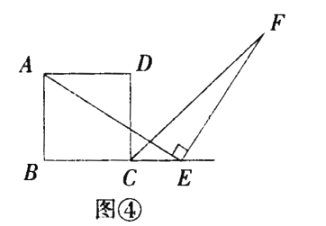
(2)探究2:小强继续探索,如图③,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立小强进一步还想试试,如图④,若把条件“点E是边BC的中点”为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF仍然成立请你选择图③或图④中的一种情况写出证明过程给小强看.
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
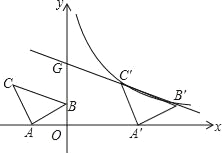
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(﹣2,0),B(0,1).
(1)求点C的坐标;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B'、C'正好落在某反比例函数图象上.请求出这个反比例函数和此时的直线B'C'的解析式.
(3)若把上一问中的反比例函数记为y1,点B′,C′所在的直线记为y2,请直接写出在第一象限内当y1<y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用棋子摆出下列一组图形:
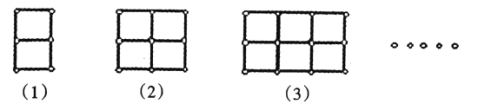
(1)填写下表:
图形编号 | 1 | 2 | 3 | 4 | 5 | 6 |
图形中的棋子 |
(2)照这样的方式摆下去,写出摆第![]() 个图形棋子的枚数;(用含
个图形棋子的枚数;(用含![]() 的代数式表示).
的代数式表示).
(3)试计算第672个图形棋子的枚数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列分式方程解应用题:今年植树节,某校师生到距学校20千米的公路旁植树,一班师生骑自行车先走,走了16千米后,二班师生乘汽车出发,结果同时到达.已知汽车的速度比自行车的速度每小时快60千米,求两种车的速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为![]() 、宽为
、宽为![]() 的长方形(其中
的长方形(其中![]() ,
,![]() 均为正数,且
均为正数,且![]() ),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
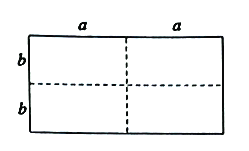
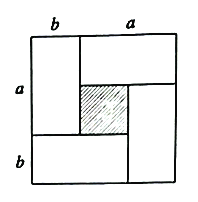
图1 图2
(1)图2中大正方形的边长为 ;小正方形(阴影部分)的边长为 .(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)仔细观察图2,请你写出下列三个代数式:![]() 所表示的图形面积之间的相等关系,并选取适合
所表示的图形面积之间的相等关系,并选取适合![]() ,
,![]() 的数值加以验证.
的数值加以验证.
(3)已知![]() .则代数式
.则代数式![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了培养学生勤俭节约的意识,从小养成良好的生活习惯.某校随机抽查部分初中生对勤俭节约的态度(态度分为:赞成、无所谓、反对),并对抽查对象的态度绘制成了图1和图2两个统计图(统计图不完整),请根据图中的信息解答下列问题:
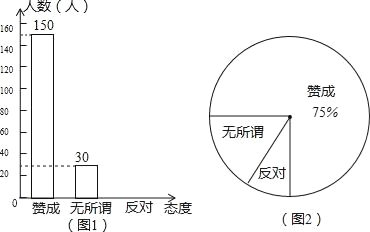
(1)此次共抽查 名学生;
(2)持反对意见的学生人数占整体的 %,无所谓意见的学生人数占整体的 %;
(3)估计该校1200名初中生中,大约有 名学生持反对态度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣8)﹣(﹣5)+(﹣2)
(2)﹣12×2+(﹣2)2÷4﹣(﹣3)
(3)化简求值:3(ab2﹣2a2 b)﹣2(ab2﹣a2 b),其中a=-1,b=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市从2018年1月1日开始,禁止燃油助力车上路,于是电动自行车的市场需求量日渐增多.某商店计划最多投入8万元购进A、B两种型号的电动自行车共30辆,其中每辆B型电动自行车比每辆A型电动自行车多500元.用5万元购进的A型电动自行车与用6万元购进的B型电动自行车数量一样.
(1)求A、B两种型号电动自行车的进货单价;
(2)若A型电动自行车每辆售价为2800元,B型电动自行车每辆售价为3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.写出y与m之间的函数关系式;
(3)在(2)的条件下,该商店如何进货才能获得最大利润?此时最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com