
【题目】列分式方程解应用题:今年植树节,某校师生到距学校20千米的公路旁植树,一班师生骑自行车先走,走了16千米后,二班师生乘汽车出发,结果同时到达.已知汽车的速度比自行车的速度每小时快60千米,求两种车的速度各是多少?
科目:初中数学 来源: 题型:
【题目】根据下列解题过程填空:
如图,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线,
的平分线,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

解:∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ①
① ![]() ②
② ![]() ,
,
∴![]() ③
③ ![]() ④
④ ![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ⑤
⑤ ![]() ④
④ ![]() ,
,
∴![]() ⑦
⑦ ![]() ⑧
⑧ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程|x2﹣x|﹣a=0,给出下列四个结论:①存在实数a,使得方程恰有2个不同的实根; ②存在实数a,使得方程恰有3个不同的实根;③存在实数a,使得方程恰有4个不同的实根;④存在实数a,使得方程恰有6个不同的实根;其中正确的结论个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘对本班同学的业余兴趣爱好进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.
请你根据图中提供的信息,解答下列问题:
(1)在图1中,将“书画”部分的图形补充完整;
(2)在图2中,求出“球类”部分所对应的圆心角的度数,并分别写出爱好“音乐”、“书画”、“其它”的人数占本班学生数的百分数;
(3)观察图1和图2,你能得出哪些结论(只要写出一条结论).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面,观察下列图形,探究并解答问题:
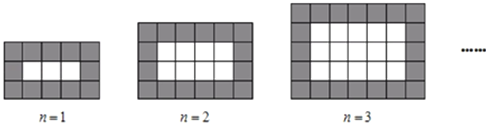
(1)在第4个图中,共有白色瓷砖______块;在第![]() 个图中,共有白色瓷砖_____块;
个图中,共有白色瓷砖_____块;
(2)试用含![]() 的代数式表示在第
的代数式表示在第![]() 个图中共有瓷砖的块数;
个图中共有瓷砖的块数;
(3)如果每块黑瓷砖35元,每块白瓷砖50元,当![]() 时,求铺设长方形地面共需花多少钱购买瓷砖?
时,求铺设长方形地面共需花多少钱购买瓷砖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20立方米时,按2元/立方米计费;月用水量超过20立方米时,其中的20立方米仍按2元/立方米收费,超过部分按2.6元/立方米计费.设每户家庭用水量为x立方米时,应交水费y元.
(1)当![]() 时,y= (用含x的代数式表示);
时,y= (用含x的代数式表示);
当![]() 时,y= (用含x的代数式表示);
时,y= (用含x的代数式表示);
(2)小明家第二季度交纳水费的情况如下:
月份 | 四月份 | 五月份 | 六月份 |
交费金额 | 30元 | 34元 | 47.8元 |
小明家这个季度共用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形的外角平分线
交正方形的外角平分线![]() 于点
于点![]() 请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
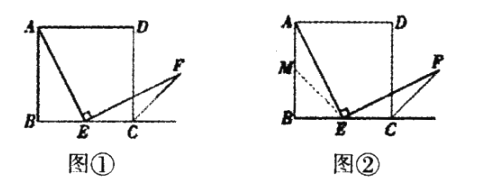
(1)探究1:小强看到图①后,很快发现![]() 这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明
这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明![]() 就行了.随即小强写出了如下的证明过程:
就行了.随即小强写出了如下的证明过程:
证明:如图②,取AB的中点M,连接EM.
∵![]()
∴![]()
又∵![]()
∴![]()
∵点E、M分别为正方形的边BC和AB的中点,
∴![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴![]()
又∵![]() 是正方形外角的平分线,
是正方形外角的平分线,
∴![]() ,∴
,∴![]()
∴![]()
∴![]() ,
,
∴![]()
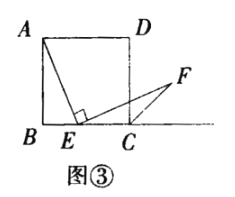
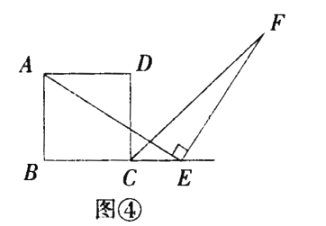
(2)探究2:小强继续探索,如图③,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立小强进一步还想试试,如图④,若把条件“点E是边BC的中点”为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF仍然成立请你选择图③或图④中的一种情况写出证明过程给小强看.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小虫从点A出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的路程依次为:(单位:cm)①+5,②-3,③+10,④-8,⑤-6,⑥+11,⑦-9.
(1)小虫最后是否回到出发点A,说明理由;
(2)小虫在第几次爬行后离点A最远,此时距离点A多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,那么小虫一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com