
ĄūĖâÄŋĄŋČôąäÁŋzĘĮąäÁŋyĩÄšŊĘýĢŽÍŽĘąąäÁŋyĘĮąäÁŋxĩÄšŊĘýĢŽÄĮÃīÎŌÃĮ°ŅąäÁŋz―ÐŨöąäÁŋxĩÄĄ°ĩüīúšŊĘýĄą.
ĀýČįĢšz2y3ĢŽyx1ĢŽÔōz2x132x1ĢŽÄĮÃīz2x1ūÍĘĮzÓëxÖŪžäĩÄĄ°ĩüīúšŊĘýĄą―âÎöĘ―.
ĢĻ1ĢĐĩą2006x2020ĘąĢŽzy2ĢŽ![]() ĢŽĮëĮóģözÓëxÖŪžäĩÄĄ°ĩüīúšŊĘýĄąĩÄ―âÎöĘ―ž°zĩÄŨîÐĄÖĩĢŧ
ĢŽĮëĮóģözÓëxÖŪžäĩÄĄ°ĩüīúšŊĘýĄąĩÄ―âÎöĘ―ž°zĩÄŨîÐĄÖĩĢŧ
ĢĻ2ĢĐČôz2yaĢŽyax24axba0ĢŽĩą1x3ĘąĢŽĄ°ĩüīúšŊĘýĄązĩÄČĄÖĩ·ķΧΊ1z17ĢŽĮóašÍbĩÄÖĩĢŧ
ĢĻ3ĢĐŌŅÖŠŌŧīΚŊĘýyax1ūđýĩã1,2ĢŽzay2b2ycb4ĢĻÆäÖÐaĄĒbĄĒcūųΊģĢĘýĢĐĢŽīÏÃũĩÄÄãÃĮŌŧķĻÖŠĩĀĄ°ĩüīúšŊĘýĄązĘĮxĩÄķþīΚŊĘýĢŽČôx1ĄĒx2ĢĻx1x2ĢĐĘĮĄ°ĩüīúšŊĘýĄąz3ĩÄÁ―ļöļųĢŽĩãx3,2ĘĮĄ°ĩüīúšŊĘýĄązĩÄķĨĩãĢŽķøĮŌx1ĄĒx2ĄĒx3ŧđĘĮŌŧļöÖą―ĮČý―ĮÐÎĩÄČýĖõąßģĪĢŽĮëÆÆ―âĄ°ĩüīúšŊĘýĄązđØÓÚxĩÄšŊĘý―âÎöĘ―.
Ąūīð°ļĄŋĢĻ1ĢĐz= -![]() x+6Ģŧ-1004ĢŧĢĻ2ĢĐ
x+6Ģŧ-1004ĢŧĢĻ2ĢĐ ŧō
ŧō ĢŧĢĻ3ĢĐ
ĢŧĢĻ3ĢĐ![]()
Ąū―âÎöĄŋ
ĢĻ1ĢĐ°Ņ![]() īúČëzy2ÖÐŧŊžōžīŋÉĩÃģöīð°ļĢŧ
īúČëzy2ÖÐŧŊžōžīŋÉĩÃģöīð°ļĢŧ
ĢĻ2ĢĐ°Ņyax24axba0īúČëz2yaÕûĀíĩÃz=2a(x-2) 2-7a+2b,ÔŲ·ÖÁ―ÖÖĮéŋöĖÖÂÛĢŽ·Öąðĩ÷―ģĖŨé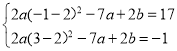 šÍ
šÍ ĢŽĮó―âžīŋÉĩÃĢŧ
ĢŽĮó―âžīŋÉĩÃĢŧ
ĢĻ3ĢĐ°ŅĢĻ1ĢŽ2ĢĐīúČëy=ax+1―âĩÃa=1ĢŽĩÃģöy=x+1ĢŽÔŲ―Ŧy=x+1īúČëz=ay2+ĢĻb-2ĢĐy+c-b+4ĩÃ![]() ĢŽļųūÝĩãx3,2ĘĮĄ°ĩüīúšŊĘýĄązĩÄķĨĩãĩÃģö
ĢŽļųūÝĩãx3,2ĘĮĄ°ĩüīúšŊĘýĄązĩÄķĨĩãĩÃģö![]()
![]() ĢŽÔŲļųūÝĩąz=3ĘąĢŽ
ĢŽÔŲļųūÝĩąz=3ĘąĢŽ ![]() ―âĩÃ
―âĩÃ![]() ĢŽÓÖx1ĄĒx2ĄĒx3ĘĮŌŧļöÖą―ĮČý―ĮÐÎĩÄČýĖõąßģĪĩÃ
ĢŽÓÖx1ĄĒx2ĄĒx3ĘĮŌŧļöÖą―ĮČý―ĮÐÎĩÄČýĖõąßģĪĩÃ![]() ĢŽīúČë―âĩÃb=-8,c=15,īÓķøĩÃ―âĄĢ
ĢŽīúČë―âĩÃb=-8,c=15,īÓķøĩÃ―âĄĢ
―âĢšĢĻ1ĢĐ°Ņ![]() īúČëzy2ÖÐĩÃĢš
īúČëzy2ÖÐĩÃĢš
zĢĻ![]() ĢĐ2= -
ĢĐ2= -![]() x+6
x+6
Ąß-![]() Ģž0ĢŽ
Ģž0ĢŽ
ĄāzËæŨÅxĩÄÔöīóķøžõÐĄĢŽ
Ąß2006 x2020 ĢŽ
Ąāĩąx=2020ĘąĢŽzÓÐŨîÐĄÖĩĢŽŨîÐĄÖĩΊz= -![]() ĄÁ2020+6=-1004
ĄÁ2020+6=-1004
đĘīð°ļΊĢšz= -![]() x+6Ģŧ-1004
x+6Ģŧ-1004
ĢĻ2ĢĐ°Ņyax24axba0īúČëz2yaĢŽĩÃ
z2ĢĻax24axbĢĐa
=2ax28axbaĢŽ
=2a(x-2) 2-7a+2b
ÕâĘĮŌŧļöķþīΚŊĘýĢŽÍžÏóĩÄķÔģÆÖáĘĮÖąÏßx=2ĢŽ
ĩąaĢū0ĘąĢŽÓÉšŊĘýÍžÏóĩÄÐÔÖĘŋÉĩÃx=-1ĘąĢŽz=17;x=3ĘąĢŽz=-1;
Ąā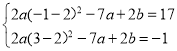
―âĩÃ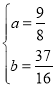
ĩąaĢž0ĘąĢŽÓÉšŊĘýÍžÏóĩÄÐÔÖĘŋÉĩÃx=-1ĘąĢŽz=-1;x=3ĘąĢŽz=17;
Ąā
―âĩÃ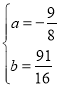
ŨÛÉÏĢŽ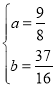 ŧō
ŧō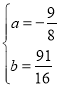
ĢĻ3ĢĐ°ŅĢĻ1ĢŽ2ĢĐīúČëy=ax+1ĩÃa+1=2
―âĩÃa=1
Ąāy=x+1
°Ņy=x+1īúČëz=ay2+ĢĻb-2ĢĐy+c-b+4ēĒÕûĀíĩÃ
![]()
Ąßĩãx3,2ĘĮĄ°ĩüīúšŊĘýĄązĩÄķĨĩã,
![]()
ÕûĀíĩÃ![]()
ĩąz=3ĘąĢŽ ![]()
―âĩÃ![]()
ÓÖĄßx1x2
Ąāx1 x3x2
ÓÖĄßx1ĄĒx2ĄĒx3ŧđĘĮŌŧļöÖą―ĮČý―ĮÐÎĩÄČýĖõąßģĪ
Ąā![]()
žī![]()
―âĩÃ![]()
Ąā![]()
°Ņ![]() īúČë
īúČë![]()
―âĩÃc=15
Ąā![]()
![]()
đĘīð°ļΊĢš![]()


 ūŦÓĒŋÚËãŋĻÏĩÁÐīð°ļ
ūŦÓĒŋÚËãŋĻÏĩÁÐīð°ļ ÓĶÓÃĖâĩãēĶÏĩÁÐīð°ļ
ÓĶÓÃĖâĩãēĶÏĩÁÐīð°ļ ŨīÔŠž°ĩÚÏĩÁÐīð°ļ
ŨīÔŠž°ĩÚÏĩÁÐīð°ļ ÍŽē―°ÂĘýÏĩÁÐīð°ļ
ÍŽē―°ÂĘýÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÐĄģæīÓĩãAģö·ĒÔÚŌŧĖõÖąÏßÉÏĀīŧØÅĀÐÐĢŽžŲķĻÏōÓŌÅĀÐÐĩÄ·ģĖžĮΊÕýĘýĢŽÏōŨóÅĀÐÐĩÄ·ģĖžĮΊļšĘýĢŽÅĀÐÐĩÄ·ģĖŌĀīÎΊĢšĢĻĩĨÎŧĢšcmĢĐĒŲ+5ĢŽĒÚ-3ĢŽĒÛ+10ĢŽĒÜ-8ĢŽĒÝ-6ĢŽĒÞ+11ĢŽĒß-9ĢŪ
ĢĻ1ĢĐÐĄģæŨîšóĘĮ·ņŧØĩ―ģö·ĒĩãAĢŽËĩÃũĀíÓÉĢŧ
ĢĻ2ĢĐÐĄģæÔÚĩÚžļīÎÅĀÐКóĀëĩãAŨîÔķĢŽīËĘąūāĀëĩãAķāÉŲĀåÃŨĢŋ
ĢĻ3ĢĐÔÚÅĀÐÐđýģĖÖÐĢŽČįđûÃŋÅĀÐÐ1ĀåÃŨ―ąĀøŌŧÁĢÖĨÂéĢŽÄĮÃīÐĄģæŌŧđēĩÃĩ―ķāÉŲÁĢÖĨÂéĢŋ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽÔÚ ABCDÖÐĢŽCD=2ADĢŽBEĄÍADÓÚĩãEĢŽFΊDCĩÄÖÐĩãĢŽÁŽ―áEFĄĒBFĢŽÏÂÁÐ―áÂÛĢšĒŲĄÏABC=2ĄÏABFĢŧĒÚEF=BFĢŧĒÛSËÄąßÐÎDEBC=2SĄũEFBĢŧĒÜĄÏCFE=3ĄÏDEF,ÆäÖÐÕýČ·―áÂÛĩÄļöĘýđēÓÐĢĻ ĢĐ.

A. 1ļö B. 2ļö C. 3ļö D. 4ļö
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŨÛšÏÓëĖ―ūŋĢš
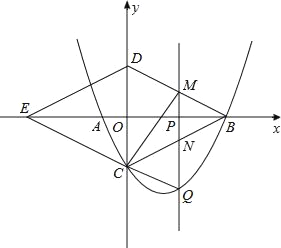
ČįÍžĢŽÅŨÎïÏßy=![]() x2Đ
x2Đ![]() xĐ4ÓëxÖá―ŧÓëAĢŽBÁ―ĩãĢĻĩãBÔÚĩãAĩÄÓŌēāĢĐĢŽÓëyÖá―ŧÓÚĩãCĢŽÁŽ―ÓBCĢŽŌÔBCΊŌŧąßĢŽĩãOΊķÔģÆÖÐÐÄŨũÁâÐÎBDECĢŽĩãPĘĮxÖáÉÏĩÄŌŧļöķŊĩãĢŽÉčĩãPĩÄŨøąęΊĢĻmĢŽ0ĢĐĢŽđýĩãPŨũxÖáĩÄīđÏßl―ŧÅŨÎïÏßÓÚĩãQĢŪ
xĐ4ÓëxÖá―ŧÓëAĢŽBÁ―ĩãĢĻĩãBÔÚĩãAĩÄÓŌēāĢĐĢŽÓëyÖá―ŧÓÚĩãCĢŽÁŽ―ÓBCĢŽŌÔBCΊŌŧąßĢŽĩãOΊķÔģÆÖÐÐÄŨũÁâÐÎBDECĢŽĩãPĘĮxÖáÉÏĩÄŌŧļöķŊĩãĢŽÉčĩãPĩÄŨøąęΊĢĻmĢŽ0ĢĐĢŽđýĩãPŨũxÖáĩÄīđÏßl―ŧÅŨÎïÏßÓÚĩãQĢŪ
ĢĻ1ĢĐĮóĩãAĢŽBĢŽCĩÄŨøąęĢŪ
ĢĻ2ĢĐĩąĩãPÔÚÏßķÎOBÉÏÔËķŊĘąĢŽÖąÏßl·Öąð―ŧBDĢŽBCÓÚĩãMĢŽNĢŪĘÔĖ―ūŋmΊšÎÖĩĘąĢŽËÄąßÐÎCQMDĘĮÆ―ÐÐËÄąßÐÎĢŽīËĘąĢŽĮëÅÐķÏËÄąßÐÎCQBMĩÄÐÎŨīĢŽēĒËĩÃũĀíÓÉĢŪ
ĢĻ3ĢĐĩąĩãPÔÚÏßķÎEBÉÏÔËķŊĘąĢŽĘĮ·ņīæÔÚĩãQĢŽĘđĄũBDQΊֹ―ĮČý―ĮÐÎĢŋČôīæÔÚĢŽĮëÖą―ÓÐīģöĩãQĩÄŨøąęĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋžÆËãĢš
ĢĻ1ĢĐĢ3Ģ7Ģŧ
ĢĻ2ĢĐ ![]() Ģŧ
Ģŧ
ĢĻ3ĢĐĢ0.5+(Ģ15.5)Ģ(Ģ17)Ģ|Ģ12|Ģŧ
ĢĻ4ĢĐ![]() Ģŧ
Ģŧ
ĢĻ5ĢĐ![]() Ģŧ
Ģŧ
ĢĻ6ĢĐ![]() (ÓÞōąã·―·ĻžÆËã)ĢŪ
(ÓÞōąã·―·ĻžÆËã)ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽĩã![]() ĘĮ
ĘĮ![]() ąß
ąß![]() ÉÏĩÄÖÐĩãĢŽ
ÉÏĩÄÖÐĩãĢŽ![]() ĢŽīđŨã·ÖąðĘĮĩã
ĢŽīđŨã·ÖąðĘĮĩã![]() .
.
(1)Čô![]() ĢŽĮóÖĪĢš
ĢŽĮóÖĪĢš![]() Ģŧ
Ģŧ
(2)Čô![]() ĢŽĮóÖĪĢšËÄąßÐÎ
ĢŽĮóÖĪĢšËÄąßÐÎ![]() ĘĮūØÐÎ.
ĘĮūØÐÎ.

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽĄũABCΊֹ―ĮČý―ĮÐÎĢŽĄÏC=90ĄãĢŽBC=2cmĢŽĄÏA=30ĄãĢŽËÄąßÐÎDEFGΊūØÐÎĢŽDE=2![]() cmĢŽEF=6cmĢŽĮŌĩãCĄĒBĄĒEĄĒFÔÚÍŽŌŧĖõÖąÏßÉÏĢŽĩãBÓëĩãEÖØšÏĢŪRtĄũABCŌÔÃŋÃë1cmĩÄËŲķČŅØūØÐÎDEFGĩÄąßEFÏōÓŌÆ―ŌÆĢŽĩąĩãCÓëĩãFÖØšÏĘąÍĢÖđĢŪÉčRtĄũABCÓëūØÐÎDEFGĩÄÖØĩþēŋ·ÖĩÄÃæŧýΊycm2ĢŽÔËķŊĘąžäxsĢŪÄÜ·īÓģycm2ÓëxsÖŪžäšŊĘýđØÏĩĩÄīóÖÂÍžÏóĘĮĢĻĄĄĄĄĢĐ
cmĢŽEF=6cmĢŽĮŌĩãCĄĒBĄĒEĄĒFÔÚÍŽŌŧĖõÖąÏßÉÏĢŽĩãBÓëĩãEÖØšÏĢŪRtĄũABCŌÔÃŋÃë1cmĩÄËŲķČŅØūØÐÎDEFGĩÄąßEFÏōÓŌÆ―ŌÆĢŽĩąĩãCÓëĩãFÖØšÏĘąÍĢÖđĢŪÉčRtĄũABCÓëūØÐÎDEFGĩÄÖØĩþēŋ·ÖĩÄÃæŧýΊycm2ĢŽÔËķŊĘąžäxsĢŪÄÜ·īÓģycm2ÓëxsÖŪžäšŊĘýđØÏĩĩÄīóÖÂÍžÏóĘĮĢĻĄĄĄĄĢĐ

A.  B.
B.  C.
C.  D.
D. 
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŨÔÖÐŅëģöĖĻĄ°ĀũÐÐ―ÚÔžĄĒ·īķÔĀË·ŅĄą°ËÏîđæķĻšóĢŽÄģÆ·ÅÆļßĩĩūÆÏúÁŋČņžõĢŽ―øČëËÄÔ·ݚóĢŽūÏúÉĖΊĀĐīóÏúÁŋĢŽÃŋÆŋūÆ![]() ąČČýÔÂ·Ý―ĩžÛ500ÔŠĢŽČįđûÂôģöÏāÍŽĘýÁŋĩÄļßĩĩūÆ
ąČČýÔÂ·Ý―ĩžÛ500ÔŠĢŽČįđûÂôģöÏāÍŽĘýÁŋĩÄļßĩĩūÆ![]() ĢŽČýÔ·ÝÏúĘÛķîΊ4.5ÍōÔŠĢŽËÄÔ·ÝÏúĘÛķîÖŧÓÐ3ÍōÔŠ.
ĢŽČýÔ·ÝÏúĘÛķîΊ4.5ÍōÔŠĢŽËÄÔ·ÝÏúĘÛķîÖŧÓÐ3ÍōÔŠ.
ĢĻ1ĢĐĮóČýÔ·ÝÃŋÆŋļßĩĩūÆ![]() ĘÛžÛΊķāÉŲÔŠĢŋ
ĘÛžÛΊķāÉŲÔŠĢŋ
ĢĻ2ĢĐΊÁËĖáļßĀûČóĢŽļÃūÏúÉĖžÆŧŪÎåÔ·Ýđš―øēŋ·ÖīóÖÚŧŊĩÄÖÐĩÍĩĩūÆ![]() ÏúĘÛ.ŌŅÖŠļßĩĩūÆ
ÏúĘÛ.ŌŅÖŠļßĩĩūÆ![]() ÃŋÆŋ―øžÛΊ800ÔŠĢŽÖÐĩÍĩĩūÆ
ÃŋÆŋ―øžÛΊ800ÔŠĢŽÖÐĩÍĩĩūÆ![]() ÃŋÆŋ―øžÛΊ400ÔŠ.ÏÖÓÃēŧģŽđý5.5ÍōÔŠĩÄÔĪËãŨĘ―ðđš―ø
ÃŋÆŋ―øžÛΊ400ÔŠ.ÏÖÓÃēŧģŽđý5.5ÍōÔŠĩÄÔĪËãŨĘ―ðđš―ø![]() ĢŽ
ĢŽ![]() Á―ÖÖūÆđē100ÆŋĢŽĮŌļßĩĩūÆ
Á―ÖÖūÆđē100ÆŋĢŽĮŌļßĩĩūÆ![]() ÖÁÉŲđš―ø35ÆŋĢŽĮëžÆËãËĩÃũÓОļÖÖ―øŧõ·―°ļĢŋ
ÖÁÉŲđš―ø35ÆŋĢŽĮëžÆËãËĩÃũÓОļÖÖ―øŧõ·―°ļĢŋ
ĢĻ3ĢĐļÃÉĖģĄžÆŧŪÎåÔÂķÔļßĩĩūÆ![]() ―øÐÐīŲÏúŧîķŊĢŽūöķĻÔÚËÄÔÂĘÛžÛŧųīĄÉÏÃŋĘÛģöŌŧÆŋļßĩĩūÆ
―øÐÐīŲÏúŧîķŊĢŽūöķĻÔÚËÄÔÂĘÛžÛŧųīĄÉÏÃŋĘÛģöŌŧÆŋļßĩĩūÆ![]() ÔŲËÍđËŋÍžÛÖĩ
ÔŲËÍđËŋÍžÛÖĩ![]() ÔŠĩÄīú―ðČŊĢŽķøÖÐĩÍĩĩūÆ
ÔŠĩÄīú―ðČŊĢŽķøÖÐĩÍĩĩūÆ![]() ÏúĘÛžÛΊ550ÔŠ/Æŋ.ŌŠĘđĢĻ2ĢĐÖÐËųÓз―°ļŧņĀûĮĄšÃÏāÍŽĢŽĮëČ·ķĻ
ÏúĘÛžÛΊ550ÔŠ/Æŋ.ŌŠĘđĢĻ2ĢĐÖÐËųÓз―°ļŧņĀûĮĄšÃÏāÍŽĢŽĮëČ·ķĻ![]() ĩÄÖĩĢŽēĒËĩÃũīËĘąÄÄÖÖ·―°ļķÔūÏúÉĖļüÓÐĀûĢŋ
ĩÄÖĩĢŽēĒËĩÃũīËĘąÄÄÖÖ·―°ļķÔūÏúÉĖļüÓÐĀûĢŋ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽĄũABCÖÐĢŽĩãOĘĮąßACÉÏŌŧļöķŊĩãĢŽđýOŨũÖąÏßMNĄÎBCĢŪÉčMN―ŧĄÏACBĩÄÆ―·ÖÏßÓÚĩãEĢŽ―ŧĄÏACBĩÄÍâ―ĮÆ―·ÖÏßÓÚĩãFĢŪ
ĢĻ1ĢĐĮóÖĪĢšOEĢ―OFĢŧ
ĢĻ2ĢĐĩąĩãOÔÚąßACÉÏÔËķŊĩ―ĘēÃīÎŧÖÃĘąĢŽËÄąßÐÎAECFĘĮūØÐÎĢŋēĒËĩÃũĀíÓÉĢŪ

ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com