
【题目】如图,在正方形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的点,且
边上的点,且![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析(2)![]()
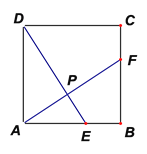
【解析】分析:(1)根据正方形的性质,用SAS证明△AED≌△BFA,得到∠ADE=∠BAF,再证∠BAF+∠AED=90°;(2)根据∠ADE=∠BAF,∠AED=∠PEA,证得△ADE∽△PAE,由对应边成比例求解.
详解:(1)∵四边形ABCD是正方形,∴AD=AB=BC,∠DAB=∠ABC=90°,
∵E,F分别是AB,BC的中点,∴AE=BF,
∴△AED≌△BFA(SAS),∴∠ADE=∠BAF,
∵∠ADE+∠AED=90°,∴∠BAF+∠AED=90°,
∴∠APE=90°,即AF⊥DE.
(2)Rt△ADE中,AD=4,AE=3,
由勾股定理得,DE=5.
∵∠ADE=∠BAF,∠AED=∠PEA,
∴△ADE∽△PAE,∴AE2=EP·ED.
∴32=5EP,EP=![]() .
.


科目:初中数学 来源: 题型:
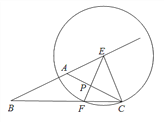
【题目】如图,己知在△ABC中,AB=AC,tanB=![]() ,BC =4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.
,BC =4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.
(1)求证:AE2=AP·AC;
(2)当点F在线段BC上,设CF=x,△PFC的面积为y,求y关于x的函数解析式及定义域;
(3)当![]() 时,求BE的长.
时,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
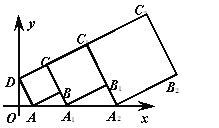
【题目】在平面坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2018个正方形的面积为( )
A. 5·![]() B. 5·
B. 5·![]() C. 5·
C. 5·![]() D. 5·
D. 5·![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
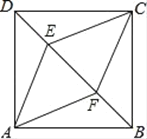
【题目】如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.
(1)判断四边形AECF是什么特殊四边形,并证明;
(2)若EF=4,DE=BF=2,求四边形AECF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
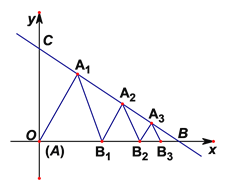
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .在
.在![]() 内依次作等边三角形使一边在
内依次作等边三角形使一边在![]() 轴上,另一个顶点在
轴上,另一个顶点在![]() 边上,作出的等边三角形第一个是
边上,作出的等边三角形第一个是![]() ,第二个是
,第二个是![]() ,第三个是
,第三个是![]() …
…
(1)![]() 的边长等于________;
的边长等于________;
(2)![]() 的边长等于________.
的边长等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
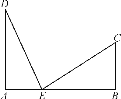
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.下表是小明家1至4月份水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 7 | 9 | 12 | 15 |
水费(元) | 14 | 18 | 26 | 35 |
(1)规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨;
(2)问该市每户每月用水规定量是多少吨?
(3)若小明家六月份应缴水费50元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
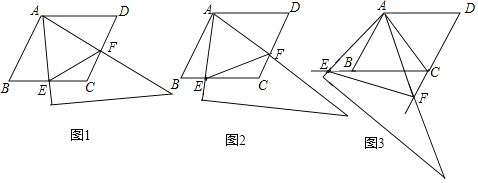
【题目】已知:四边形ABCD是菱形,AB=4,∠ABC=60°,有一足够大的含60°角的直角三角尺的60°角的顶点与菱形ABCD的顶点A重合,两边分别射线CB、DC相交于点E、F,且∠EAP=60°.
(1)如图1,当点E是线段CB的中点时,请直接判断△AEF的形状是 .
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
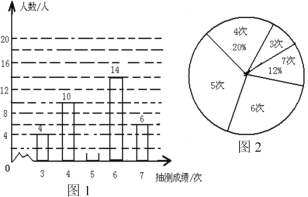
【题目】为了了解某校七年级男生的体能情况,体育老师随即抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2尚不完整的统计图。
(1)本次抽测的男生有 人;
(2)请你将图1的统计图补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,则该校350名九年级男生中,估计有多少人体能达标?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com