
【题目】已知反比例函数![]() 和一次函数
和一次函数![]() ,其中一次
,其中一次
函数图象经过(a,b)与(a+1,b+k)两点.
(1) 求反比例函数的解析式.
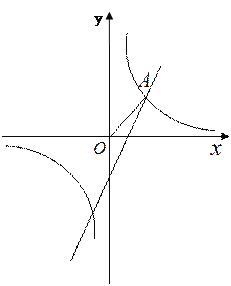
(2) 如图,已知点A是第一象限内上述两个函数图象的交点,求A点坐标.
(3) 利用(2)的结果,请问:在X轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
【答案】(1)反比例函数的解析式为y=![]()
(2)A的坐标为(1,1)
(3)存在,符合条件的点有4个,分别是(![]() ,0),(-
,0),(-![]() ,0),(2,0),(1,0).
,0),(2,0),(1,0).
【解析】
(1)把过一次函数的两个点代入一次函数,即可求得k,进而求得反比例函数的解析式.
(2)同时在这两个函数解析式上,让这两个函数组成方程组求解即可.
(3)应先求出OA的距离,然后根据:OA=OP,OA=AP,OP=AP,分情况讨论解决.
解:(1)由题意得
![]()
解得k=2
∴反比例函数的解析式为y=![]()
(2)由![]() =2x-1
=2x-1
,解得x1=1,x2=![]()
∵A点A在第一象限
点A的坐标为(1,1)
(3)OA=![]() ,OA与x轴所夹锐角为45°,
,OA与x轴所夹锐角为45°,
①当OA为腰时,由OA=OP1得P1(![]() ,0),
,0),
由OA=OP2得P2(-![]() ,0);
,0);
由OA=AP3得P3(2,0).
②当OA为底时,OP4=AP4得P4(1,0).
∴符合条件的点有4个,分别是(![]() ,0),(-
,0),(-![]() ,0),(2,0),(1,0).
,0),(2,0),(1,0).


科目:初中数学 来源: 题型:
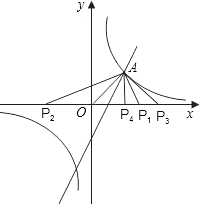
【题目】如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点三点![]() ,
,![]() ,
,![]() .
.

(1)求抛物线的解析式和对称轴;
(2)![]() 是抛物线对称轴上的一点,求满足
是抛物线对称轴上的一点,求满足![]() 的值为最小的点
的值为最小的点![]() 坐标(请在图1中探索);
坐标(请在图1中探索);
(3)在第四象限的抛物线上是否存在点![]() ,使四边形
,使四边形![]() 是以
是以![]() 为对角线且面积为
为对角线且面积为![]() 的平行四边形?若存在,请求出点
的平行四边形?若存在,请求出点![]() 坐标,若不存在请说明理由.(请在图2中探索)
坐标,若不存在请说明理由.(请在图2中探索)
查看答案和解析>>
科目:初中数学 来源: 题型:
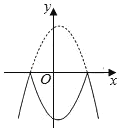
【题目】如图,将抛物线y=x2+2x+8的图象x轴上方的部分沿x轴折到x轴下方,图象的其余部分不变,得到一个新图象(实线部分);点P(a,ka-1)在该函数上,若这样的点P恰好有3个,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
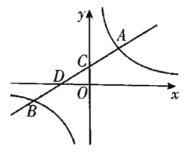
【题目】如图,已知一次函数y1=kx+b与反比例函数y2 =![]() 图象在第一、第三象限分别交于A(3,4),B(a,-2)两点,直线AB与y轴,x轴分别交于C,D两点.
图象在第一、第三象限分别交于A(3,4),B(a,-2)两点,直线AB与y轴,x轴分别交于C,D两点.
(1)求一次函数和反比例函数的解析式;
(2)比较线段AD、BC大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
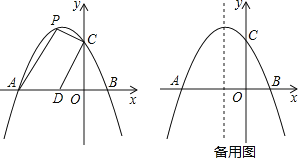
【题目】如图,抛物线y=ax2+bx+2交x轴于点A(-3,0)和点B(1,0),交y轴于点C.
(1)求这个抛物线的函数表达式.
(2)点D的坐标为(-1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.
(3)点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠MNO为直角?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
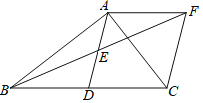
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的情况下,点M在AC线段上移动,请直接回答,当点M移动到什么位置时,MB+MD有最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
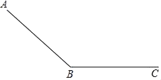
【题目】一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
A.270B.280C.375D.450
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com