
【题目】等腰三角形一腰上的高与另一腰的夹角为38°,则该等腰三角形的底角的度数为__________
【答案】64°或26°
【解析】
等腰三角形分锐角和钝角两种情况,求出每种情况的顶角的度数,再利用等边对等角的性质(两底角相等)和三角形的内角和定理,即可求出底角的度数.
①若∠A<90°,如图1所示:

∵BD⊥AC,
∴∠A+∠ABD=90°,
∵∠ABD=38°,
∴∠A=90°38°=52°,
∵AB=AC,
∴∠ABC=∠C=![]() (180°52°)=64°;
(180°52°)=64°;
②若∠A>90°,如图2所示:

同①可得:∠DAB=90°38°=52°,
∴∠BAC=180°52°=128°,
∵AB=AC,
∴∠ABC=∠C=![]() (180°128°)=26°;
(180°128°)=26°;
综上所述:等腰三角形底角的度数为64°或26°.
故答案为64°或26°.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】计算
(1)4a2b(ab-2b2-1)
(2)(x-2y)(y+2x)
(3)![]()
(4)2019×2017-20182(用简便方法计算)
(5)先化简,再求值:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且F,C,B三等分半圆,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.

(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,![]() ,
,![]() ,
,![]() ,点E为CD上一动点,经过A、C、E三点的
,点E为CD上一动点,经过A、C、E三点的![]() 交BC于点F.
交BC于点F.
(操作与发现)
![]() 当E运动到
当E运动到![]() 处,利用直尺与规作出点E与点F;
处,利用直尺与规作出点E与点F;![]() 保留作图痕迹
保留作图痕迹![]()
![]() 在
在![]() 的条件下,证明:
的条件下,证明:![]() .
.
(探索与证明)
![]() 点E运动到任何一个位置时,求证:
点E运动到任何一个位置时,求证:![]() ;
;
(延伸与应用)
![]() 点E在运动的过程中求EF的最小值.
点E在运动的过程中求EF的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆。假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股点.
(1)已知点M、N是线段AB的勾股点,若AM=1,MN=2,求BN的长;
(2)如图2,点P(a,b)是反比例函数y=![]() (x>0)上的动点,直线y=﹣x+2与坐标轴分别交于A、B两点,过点P分别向x、y轴作垂线,垂足为C、D,且交线段AB于E、F.证明:E、F是线段AB的勾股点;
(x>0)上的动点,直线y=﹣x+2与坐标轴分别交于A、B两点,过点P分别向x、y轴作垂线,垂足为C、D,且交线段AB于E、F.证明:E、F是线段AB的勾股点;
(3)如图3,已知一次函数y=﹣x+3与坐标轴交于A、B两点,与二次函数y=x2﹣4x+m交于C、D两点,若C、D是线段AB的勾股点,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
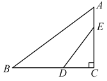
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
.点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com