
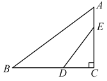
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
.点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
【答案】![]()
【解析】
把△ABC沿DE对折,点C恰好落在AB的F点处,CF与DE相交于O点,根据折叠的性质得到DE⊥CF,OC=OF,再根据等角的余角相等得∠1=∠EDC,而∠EDC=∠A,则∠1=∠A,所以FC=FA,同理可得FC=FB,于是有CF=![]() AB,OC=
AB,OC=![]() AB,然后根据正切的定义和勾股定理得到BC=4,AB=5,所以OC=
AB,然后根据正切的定义和勾股定理得到BC=4,AB=5,所以OC=![]() ,再分别在Rt△OEC和Rt△ODC中,利用正切的定义计算出OE=
,再分别在Rt△OEC和Rt△ODC中,利用正切的定义计算出OE=![]() ,OD=
,OD=![]() ,再计算OE+OD即可.
,再计算OE+OD即可.
把△ABC沿DE对折,点C恰好落在AB的F点处,CF与DE相交于O点,如图,

∴DE⊥CF,OC=OF,
∵∠EDC+∠OCD=90°,∠1+∠OCD=90°,
∴∠1=∠EDC,
而∠EDC=∠A,
∴∠1=∠A,
∴FC=FA,
同理可得FC=FB,
∴CF=![]() AB,
AB,
∴OC=![]() AB,
AB,
在Rt△ABC中,∠C=90°,AC=3,
∴tanA=![]() ,
,
∴BC=4,
∴AB=![]() =5,
=5,
∴OC=![]() ,
,
在Rt△OEC中,tan∠1=tan∠A=![]() ,
,
∴OE=![]() ,
,
在Rt△ODC中,tan∠ODC=tan∠A=![]() ,
,
∴OD=![]() ,
,
∴DE=OD+OE=![]() +
+![]() =
=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4,E为BC中点,AE⊥BC于点E,AF⊥CD于点F,CG∥AE,CG交AF于点H,交AD于点G.
(1)求菱形ABCD的面积;(2)求∠CHA的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们有时会碰上形如![]() ,
,![]() ,
,![]() 的式子,其实我们可以将其进一步分母有理化.
的式子,其实我们可以将其进一步分母有理化.
形如![]() 的式子还可以用以下方法化简:
的式子还可以用以下方法化简:![]() .(*)
.(*)
(1)请用不同的方法化简(写出化简过程):
(i)参照分母有理化的方法得![]() ______________________________;
______________________________;
(ii)参照(*)式的化简方法得![]() ______________________________.
______________________________.
(2)化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,CD、CE分别是△ABC的高和角平分线,∠BAC=α,∠B=β(α>β).

(1)若α=70°,β=40°,求∠DCE的度数;
(2)试用α、β的代数式表示∠DCE的度数(直接写出结果);
(3)如图②,若CE是△ABC外角∠ACF的平分线,交BA延长线于点E,且α﹣β=30°,求∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到一个问题:已知:如图1,在△ABC中,∠BAC=120°,∠ABC=40°,试过△ABC的一个顶点画一条直线,将此三角形分割成两个等腰三角形.
他的做法是:如图2,首先保留最小角∠C,然后过三角形顶点A画直线交BC于点D. 将∠BAC分成两个角,使∠DAC=20°,△ABC即可被分割成两个等腰三角形.
喜欢动脑筋的小明又继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
他的做法是:

如图3,先画△ADC ,使DA=DC,延长AD到点B,使△BCD也是等腰三角形,如果DC=BC,那么∠CDB =∠ABC,因为∠CDB=2∠A,所以∠ABC= 2∠A.于是小明得到了一个结论:
当三角形中有一个角是最小角的2倍时,则此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.
请你参考小明的做法继续探究:当三角形内角中的两个角满足怎样的数量关系时,此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.请直接写出你所探究出的另外两条结论(不必写出探究过程或理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙只捕捞船同时从A港出海捕鱼,甲船以每小时15![]() km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
(1)甲船从C处出发追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2016C2017B的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中, ∠C=90°,边AB的垂直平分线交AB、AC分别于点D,点E,连结BE.

(1)若∠A=40°,求∠CBE的度数.
(2)若AB=10,BC=6,求△BCE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com