
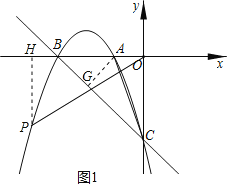
【题目】如图,抛物线![]() 与
与![]() 轴交于点A(-1,0),点B(-3,0),且OB=OC,
轴交于点A(-1,0),点B(-3,0),且OB=OC,
(1)求抛物线的解析式;
(2)点P在抛物线上,且∠POB=∠ACB,求点P的坐标;
(3)抛物线上两点M,N,点M的横坐标为m,点N的横坐标为m+4.点D是抛物线上M,N之间的动点,过点D作y轴的平行线交MN于点E.
①求DE的最大值.
②点D关于点E的对称点为F.当m为何值时,四边形MDNF为矩形?

【答案】(1)![]() ;(2)点P坐标为
;(2)点P坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;(3)①当
;(3)①当![]() 时,
时,![]() 最大值为4,②当
最大值为4,②当![]() 或
或![]() 时,四边形MDNF为矩形.
时,四边形MDNF为矩形.
![]()
【解析】
(1)已知抛物线与x轴两交点坐标,可设交点式y=a(x+1)(x+3);由OC=OB=3得C(0,-3),代入交点式即求得a=-1.
(2)由∠POB=∠ACB联想到构造相似三角形,因为求点P坐标一般会作x轴垂线PH得Rt△POH,故可过点A在BC边上作垂线AG,构造△ACG∽△POH.利用点A、B、C坐标求得AG、CG的长,由相似三角形对应边成比例推出![]() .设点P横坐标为p,则OH与PH都能用p表示,但需按P横纵坐标的正负性进行分类讨论.得到用p表示OH与PH并代入OH=2PH计算即求得p的值,进而求点P坐标.
.设点P横坐标为p,则OH与PH都能用p表示,但需按P横纵坐标的正负性进行分类讨论.得到用p表示OH与PH并代入OH=2PH计算即求得p的值,进而求点P坐标.
(3)①用m表示M、N横纵坐标,把m当常数求直线MN的解析式.设D横坐标为t,把x=t代入直线MN解析式得点E纵坐标,D与E纵坐标相减即得到用m、t表示的DE的长,把m当常数,对未知数t进行配方,即得到当t=m+2时,DE取得最大值.
②由矩形MDNF得MN=DF且MN与DF互相平分,所以E为MN中点,得到点D、E横坐标为m+2.由①得d=m+2时,DE=4,所以MN=8.用两点间距离公式用m表示MN的长,即列得方程求m的值.
解:(1)∵抛物线与x轴交于点A(-1,0),点B(-3,0)
∴设交点式y=a(x+1)(x+3)
∵OC=OB=3,点C在y轴负半轴
∴C(0,-3)
把点C代入抛物线解析式得:3a=-3
∴a=-1
∴抛物线解析式为y=-(x+1)(x+3)=-x2-4x-3
(2)如图1,过点A作AG⊥BC于点G,过点P作PH⊥x轴于点H
∴∠AGB=∠AGC=∠PHO=90°
∵∠ACB=∠POB
∴△ACG∽△POH
![]()
![]()
∵OB=OC=3,∠BOC=90°
∴∠ABC=45°,![]()
∴△ABG是等腰直角三角形
![]()
![]()
![]()
∴OH=2PH
设P(p,-p2-4p-3)
①当p<-3或-1<p<0时,点P在点B左侧或在AC之间,横纵坐标均为负数
∴OH=-p,PH=-(-p2-4p-3)=p2+4p+3
∴-p=2(p2+4p+3)
解得:![]()
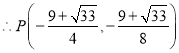 或
或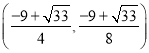
②当-3<p<-1或p>0时,点P在AB之间或在点C右侧,横纵坐标异号
∴p=2(p2+4p+3)
解得:p1=-2,p2=-![]()
∴P(-2,1)或![]()
综上所述,点P的坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;
;
(3)①如图2,
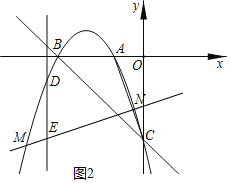
∵x=m+4时,y=-(m+4)2-4(m+4)-3=-m2-12m-35
∴M(m,-m2-4m-3),N(m+4,-m2-12m-35)
设直线MN解析式为y=kx+n
∴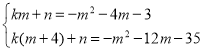
解得:![]()
∴直线MN:y=(-2m-8)x+m2+4m-3
设D(t,-t2-4t-3)(m<t<m+4)
∵DE∥y轴
∴xE=xD=t,E(t,(-2m-8)t+m2+4m-3)
∴DE=-t2-4t-3-[(-2m-8)t+m2+4m-3]=-t2+(2m+4)t-m2-4m=-[t-(
∴当t=m+2时,DE的最大值为4.
②如图3,
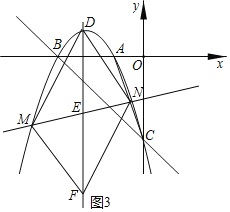
∵D、F关于点E对称
∴DE=EF
∵四边形MDNF是矩形
∴MN=DF,且MN与DF互相平分
∴DE= ![]() MN,E为MN中点
MN,E为MN中点
![]()
由①得当d=m+2时,DE=4
∴MN=2DE=8
∴(m+4-m)2+[-m2-12m-35-(-m2-4m-3)]2=82
解得:![]()
∴m的值为![]() 或
或![]() 时,四边形MDNF为矩形.
时,四边形MDNF为矩形.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】小明骑自行车去上学途中,经过先上坡后下坡的一段路,在这段路上所骑行的路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示.下列结论:①小明上学途中下坡路的长为1800米;②小明上学途中上坡速度为150米/分,下坡速度为200米/分;③如果小明放学后按原路返回,且往返过程中,上、下坡的速度都相同,则小明返回时经过这段路比上学时多用1分钟;④如果小明放学后按原路返回,返回所用时间与上学所用时间相等,且返回时下坡速度是上坡速度的1.5倍,则返回时上坡速度是160米/分其中正确的有( )
(分钟)之间的函数关系如图所示.下列结论:①小明上学途中下坡路的长为1800米;②小明上学途中上坡速度为150米/分,下坡速度为200米/分;③如果小明放学后按原路返回,且往返过程中,上、下坡的速度都相同,则小明返回时经过这段路比上学时多用1分钟;④如果小明放学后按原路返回,返回所用时间与上学所用时间相等,且返回时下坡速度是上坡速度的1.5倍,则返回时上坡速度是160米/分其中正确的有( )
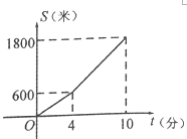
A.①④B.②③C.②③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个批发店销售同一种苹果.在甲批发店,不论一次购买数量是多少,价格均为6元/kg.在乙批发店,一次购买数量不超过元50kg时,价格为7元/kg;一次购买数量超过50kg时,其中有50kg的价格仍为7元/kg,超出50kg部分的价格为5元/kg.设小王在同一个批发店一次购买苹果的数量为![]()
![]() .
.
(Ⅰ)根据题意填表:
一次购买数量/kg | 30 | 50 | 150 | … |
甲批发店花费/元 | 300 | … | ||
乙批发店花费/元 | 350 | … |
(Ⅱ)设在甲批发店花费![]() 元,在乙批发店花费
元,在乙批发店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为____________kg;
②若小王在同一个批发店一次购买苹果的数量为120kg,则他在甲、乙两个批发店中的________批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的________批发店购买数量多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四张正面分别写有1、2、3、4的不透明卡片,它们的背面完全相同,现把它们洗匀,背面朝上放置后,开始游戏![]() 游戏规则如下:
游戏规则如下:
连摸三次,每次随机摸出一张卡片,并翻开记下卡片上的数字,每次摸出后不放回,如果第三次摸出的卡片上的数字,正好介于第一、二次摸出的卡片上的数字之间,则游戏胜出,否则,游戏失败![]() 问:
问:
![]() 若已知小明第一次摸出的数字是4,第二次摸出的数字是2,在这种情况下,小明继续游戏,可以获胜的概率为______.
若已知小明第一次摸出的数字是4,第二次摸出的数字是2,在这种情况下,小明继续游戏,可以获胜的概率为______.
![]() 若已知小明第一次摸出的数字是3,求在这种情况下,小明继续游戏,可以获胜的概率
若已知小明第一次摸出的数字是3,求在这种情况下,小明继续游戏,可以获胜的概率![]() 要求列表或用树状图求
要求列表或用树状图求![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
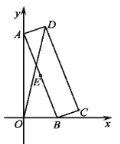
【题目】如图,矩形硬纸片ABCD的顶点A在![]() 轴的正半轴及原点上滑动,顶点B在
轴的正半轴及原点上滑动,顶点B在![]() 轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为
轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为![]() ,其中正确的结论是_________(填写序号).
,其中正确的结论是_________(填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
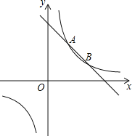
【题目】如图,反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标和点B的纵坐标都是1.
的图象和一次函数的图象交于A、B两点,点A的横坐标和点B的纵坐标都是1.
(1)在第一象限内,写出关于x的不等式kx+b≥![]() 的解集 ;
的解集 ;
(2)求一次函数的表达式;
(3)若点P(m,n)在反比例函数图象上,且关于y轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
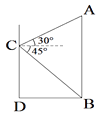
【题目】某数学兴趣小组的同学在一次活动中,为了测量某建筑物AB的高,他们来到另一建筑物CD上的点C处进行观察,如图所示,他们测得建筑物AB顶部A的仰角为30°,底部B的俯角为45°,已知建筑物AB、CD的距离DB为12m,求建筑物AB的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
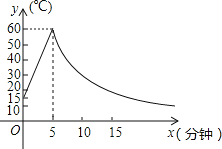
【题目】制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
(3)该种材料温度维持在40℃以上(包括40℃)的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
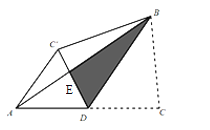
【题目】如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC′沿BD翻折,得到△![]() ,DC与AB交于点E,连结
,DC与AB交于点E,连结![]() ,若AD=AC′=2,BD=3则点D到BC的距离为( )
,若AD=AC′=2,BD=3则点D到BC的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com