
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,求出∠PFD与∠AEM的数量关系;
(2)当△PMN所放位置如图②所示时,求证:∠PFD-∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=15°,∠PEB=30°,求∠N的度数.

【答案】(1)∠PFD+∠AEM=90°;(2)见解析;(3)∠N=45°.
【解析】
(1)如图,由平行线的性质得出∠PFD=∠NPH,∠AEM=∠HPM,即可得出结果;
(2)设PN交AB于点G,由平行线的性质得出∠PFD=∠PGB,再由三角形的外角等于与它不相邻的两个内角的和即可得出结果;
(3)由三角形的外角等于与它不相邻的两个内角的和求出∠PFD=90°+∠PEB=120°,再由平行线的性质得出∠NFO=120°,然后由三角形的内角和定理即可得出结果.
解:(1)如图,过点P作PH∥AB.
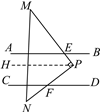
∵AB∥CD,
∴PH∥CD,
∴∠PFD=∠NPH,∠AEM=∠HPM.
∵∠MPN=90°,
∴∠NPH+∠HPM=90°,
∴∠PFD+∠AEM=90°.
(2)证明:设PN交AB于点G.
∵AB∥CD,
∴∠PFD=∠PGB.
∵∠PGB-∠PEB=90°,∠PEB=∠AEM,
∴∠PFD-∠AEM=90°.
(3)由(2)得,∠PFD=90°+∠PEB=120°,
∴∠NFO=120°,
∴∠N=180°-∠DON-∠NFO=45°.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
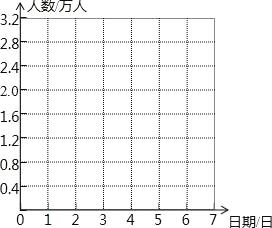
【题目】“十一”黄金周期间,深圳世界之窗风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | ﹣0.4 | ﹣0.8 | +0.2 | ﹣1.2 |
(1)请判断七天内游客人数最多的是 日,最少的是 日.
(2)以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=5,BD=3,则线段CE的长为( )

A. 3 B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
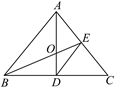
【题目】如图,△ABC的角平分线AD,中线BE相交于点O,有下列结论:①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线.其中正确结论的序号是 ________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一台自动测温仪记录的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )

A. 凌晨4时气温最低为-3℃
B. 14时气温最高为8℃
C. 从0时至14时,气温随时间增长而上升
D. 从14时至24时,气温随时间增长而下降
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,延长AB到C,使BC=![]() AB,D为AC的中点,若BD=6.
AB,D为AC的中点,若BD=6.
(1)画出图形,求AB的长;
(2)若点E在直线AB上,AE=3,求线段ED的长;
(3)若点F在直线AB上,AF=k,求线段FD的长(请直接写出答案、用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG; (2)OG= ![]() BC; ( 3)OGE是等边三角形; ( 4)SAOE=
BC; ( 3)OGE是等边三角形; ( 4)SAOE= ![]() S矩形ABCD
S矩形ABCD
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com